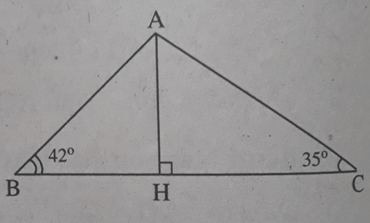
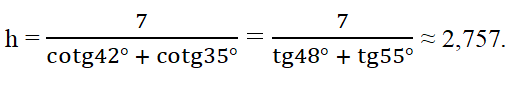Cho tam giác ABC có BC = 7, (ABC) = , (ACB) = . Gọi H là chân đường cao của tam giác ABC kẻ từ A. Hãy tính AH (làm tròn kết quả đến chữ số thập phân thứ ba).
Câu hỏi trong đề: Giải Sách Bài Tập Toán 9 Tập 1 !!
Quảng cáo
Trả lời:
Đặt AH = h thì rõ ràng BH = h.cotg (ABH) = h. cotg
CH = h.cotg (ACH) = h.cotg (để ý rằng H thuộc đoạn BC vì , đều là góc nhọn).
Do đó: 7 = BC = BH + CH = h(cotg + cotg), suy ra
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
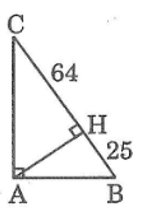
Theo hệ thức liên hệ giữa đường cao và hình chiếu, ta có:
Suy ra:
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.