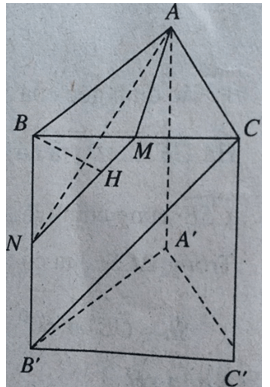
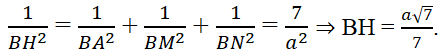Cho lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác vuông với AB = BC = a, cạnh bên . Gọi M là trung điểm BC. Tính khoảng cách giữa hai đường thẳng AM, B'C.
Câu hỏi trong đề: Giải sách bài tập Hình học 11 !!
Quảng cáo
Trả lời:
Gọi N là trung điểm của BB’, ta có: CB’ // MN nên CB’ // (AMN). Như vậy
d(BC’, AM) = d(B’, (AMN)) = d(B, (AMN))
(vì B, B’ đối xứng qua N ∈ (AMN)).
Hạ BH ⊥ (AMN), ta có d(B, (AMN)) = BH.
Nhận xét:
Tứ diện B.AMN có ba cạnh BA, BM, BN vuông góc nhau từng đôi một nên
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Trọng tâm Sử, Địa, GD KTPL 11 cho cả 3 bộ Kết nối, Chân trời, Cánh diều VietJack - Sách 2025 ( 38.000₫ )
- Sách - Sổ tay kiến thức trọng tâm Vật lí 11 VietJack - Sách 2025 theo chương trình mới cho 2k8 ( 45.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
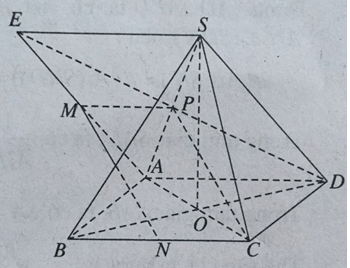
Gọi P là trung điểm SA, ta có MPCN là hình bình hành.
Như vậy MN // PC, suy ra MN // (SAC).
Do BD ⊥ (SAC) nên BD ⊥ MN.
Ta có: d(MN, AC) = d(N, (SAC))
Mà C ∈(SAC) & CN/CB = 1/2
Nên d(N, (SAC)) = 1/2 d(B, (SAC)) = 1/2 BO (O là giao điểm của AC và BD).
Vậy d(N, (SAC)) = 1/4a√2.
Lời giải
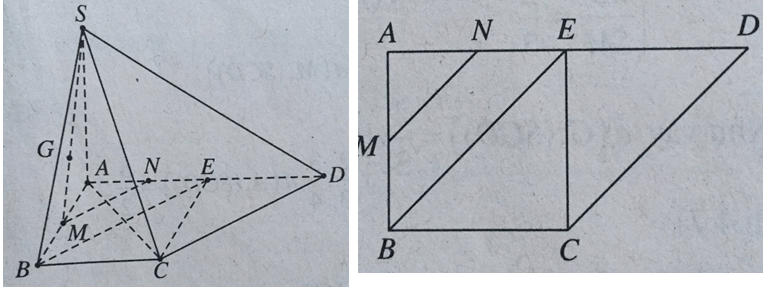
+ Xác định góc của SC với (SAD).
Hạ CE ⊥ AD, ta có E là trung điểm AD và CE ⊥ (SAD) nên ∠(CSE) = .
∠(CSE) cũng chính là góc giữa SC và mp(SAD).
Trong ΔCSE, ta có:
.
Nhận xét
Gọi M, N lần lượt là trung điểm của AB và AE.
Ta có MN // BE nên MN // CD. Như vậy MN // (SCD). Ta suy ra
d(M,(SCD)) = d(N,(SCD)).
Mà DN/DA = 3/4 nên d(N,(SCD)) = 3/4 d(A,(SCD))
+ Xác định khoảng cách từ A đến (SCD).
Vì vậy tam giác ACD vuông cân tại C nên CD vuông góc với AC.
CD ⊥ AC & CD ⊥ SA ⇒ CD ⊥ (SAC) ⇒ (SCD) ⊥ (SAC).
Hạ AH ⊥ SC, ta có AH ⊥ (SCD).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.