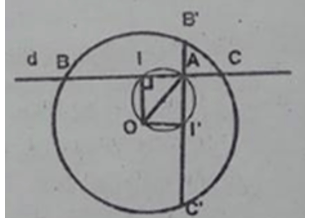
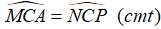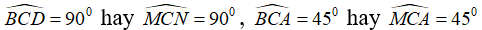Cho đường tròn tâm O bán kính R và điểm A (khác O) ở trong đường tròn đó. Một đường thẳng d thay đổi, luôn đi qua A, cắt đường tròn đã cho tại hai điểm là B và C. Tìm quỹ tích trung điểm I của đoạn thẳng BC.
Câu hỏi trong đề: Giải Sách Bài Tập Toán 9 Tập 2 !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Chứng minh thuận:
Đường tròn (O) cho trước, điểm A cố định nên OA có độ dài không đổi.
ΔOBC cân tại O (vì OB = OC bán kính)
IB = IC (gt) nên OI là đường trung tuyến vừa là đường cao
OI ⊥ BC
Góc OIA =
Đường thẳng d thay đổi nên B, C thay đổi thì I thay đổi tạo với 2 đầu đoạn OA cố định góc góc OIA = . Vậy I chuyển động trên đường tròn đường kính OA.
Chứng minh đảo: Lấy điểm I’ bất kỳ trên đường tròn đường kính AO. Đường thẳng AI’ cắt đường tròn (O) tại 2 điểm B’ và C’.
Ta chứng minh: I’B = I’C’.
Trong đường tròn đường kính AO ta có góc OI'A = (góc nội tiếp chắn nửa đường tròn)
OI'⊥ B'C'
I'B' = I'C' (đường kính vuông góc với dây cung)
Vậy quỹ tích các điểm I là trung điểm của dây BC của đường tròn tâm O khi BC quay xung quanh điểm A cố định là đường tròn đường kính AO.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
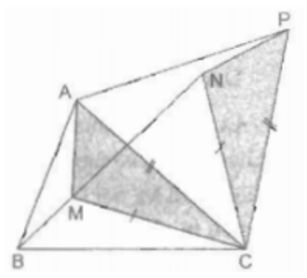
Trong ABC ta lấy điểm M. Nối MA, MB, MC.
Ta cần làm xuất hiện tổng MA + MB + MC sau đó tìm điều kiện để tổng đó nhỏ nhất.
Lấy MC làm cạnh dựng trên nửa mặt phẳng bờ BC chứa điểm A tam giác đều MCN. Suy ra: CM = MN.
Lấy AC làm cạnh dựng trên nửa mặt phẳng bờ AC không chứa điểm B tam giác đều APC. Khi đó, CA = CP
Xét AMC và PNC:
CM = CN (vì ΔMCN đều)
CA = CP (vì ΔAPC đều)
Suy ra: AMC = PNC (c.g.c)
⇒ PN = AM
MA + MB + MC = NP + MB + MN
Ta có ABC cho trước nên điểm P cố định nên BM + MN + NP ngắn nhất khi 4 điểm B, M, N, P thẳng hàng.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
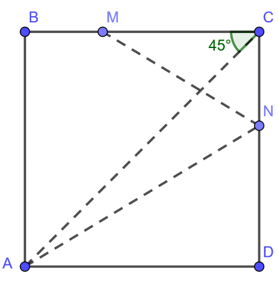
Phân tích: Vì ABCD là hình vuông nên:
Ta có, ba điểm A, M, N cố định nên bài toán quy về việc dựng đỉnh C. Đỉnh C là giao điểm của :
- Cung chứa góc dựng trên đoạn thẳng MN
- Cung chứa góc dựng trên đoạn thẳng AM
Cách dựng:
- Dựng cung chứa góc trên đoạn MN
- Dựng cung chứa góc trên đoạn AM
Hai cung cắt nhau tại C
- Nối CM ,CN
- kẻ AB ⊥ CM tại B , AD ⊥ CN tại D
Tứ giác ABCD là hình vuông cần dựng
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập