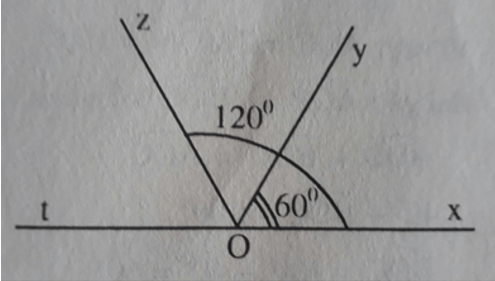
Trên cùng một nửa mặt phẳng bờ Ox, vẽ các tia Oy, Oz sao cho = , =
a) Chứng minh rằng Oy là tia phân giác của góc xOz
b) Gọi Ot là tia đối của tia Ox. Chứng minh rằng Oz là tia phân giác của góc yOt.
Câu hỏi trong đề: Đề kiểm tra 1 tiết Chương 2: Góc !!
Quảng cáo
Trả lời:
a) Trên cùng một nửa mặt phẳng bờ chứa tia Ox có hai tia Oy, Oz và < ( vì < ) nên tia Oy nằm giữa hai tia Ox, Oz
Ta có:
+ =
+ =
= - =
Tia Oy nằm giữa hai tia Ox, Oz và = ( = )
Vậy tia Oy là phân giác của góc xOz
b) Hai góc xOz và zOt kề bù , nên: + =
+ =
= - =
Tia Oz nằm giữa hai tia Oy, Ot và = ( = )
Vậy tia Oz là phân giác của góc yOt
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
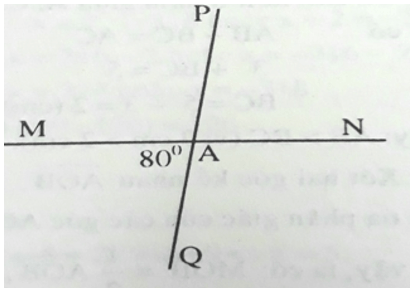
Ta có: và kề bù nên:
+ =
+ =
= - =
Và và kề bù nên:
+ =
+ =
= - =
Lời giải
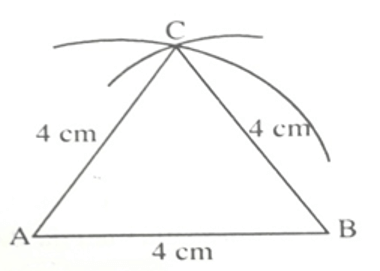
- Vẽ đoạn thẳng AB = 4 cm
- Vẽ cung tròn tâm A bán kính 4 cm
- Vẽ cung tròn tâm B bán kính 4 cm, cắt cung tròn tâm A bán kính 4 cm tại C.
- Vẽ các đoạn thẳng AC, BC. Ta được tam giác ABC.
Đo góc có BAC = ABC = ACB =
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.