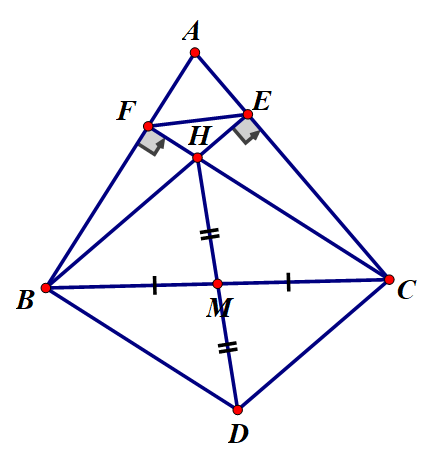
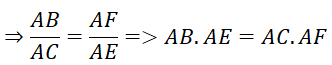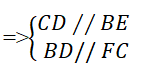Cho tam giác ABC, hai đường cao BE và CF cắt nhau tại H. Gọi D là điểm đối xứng của H qua trung điểm M của BC
a) Chứng minh tứ giác BFEC nội tiếp được đường tròn
Câu hỏi trong đề: Đề kiểm tra 15 phút Toán 9 Chương 3 Hình học có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
a) Xét tứ giác BFEC có:
∠(BFC) = ∠(BEC) = (gt)
Mà 2 góc này cùng nhìn cạnh BC
⇒ Tứ giác BFEC nội tiếp được đường tròn
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
b) Xét ΔABF và ΔACE có:
∠(BEA) = ∠(CFA) = (gt)
∠(BAC ) chung
⇒ ΔABF ∼ ΔACE (g.g)
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
c) Xét tứ giác BHCD có:
M là trung điểm của 2 đường chéo HD và BC
⇒ Tứ giác BHCD là hình bình hành
Mà BE ⊥ AC ; FC ⊥ AB
⇒ CD ⊥ AC ; DB ⊥ AB
Xét tứ giác ABDC có:
∠(ABD) = ∠(ACD) =
∠(ABD ) + ∠(ACD) =
⇒ Tứ giác ABDC nội tiếp được đường tròn
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập