Cho tam giác ABC, trên cạnh AB và AC lấy các điểm tương ứng D và E. Đường thẳng song song với AC qua D cắt BE tại I, đường thẳng song song với AB qua E cắt CD tại K. Chứng minh rằng IK // BC.
Quảng cáo
Trả lời:
Giải bởi Vietjack
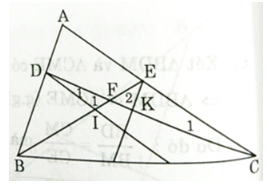
Gọi F là giao điểm của BE và CD.
Ta có DI // AC (gt) ⇒ ∠D1 = ∠C1 (so le trong)
và ∠F1 = ∠F2 (đối đỉnh)
Do đó: ΔDFI ∼ ΔCFE (g.g)
Tương tự ta có: ΔDFB ∼ ΔKFE
Từ (1), (2) ⇒ FC.FI = FB.FK
Do đó theo định lí Talét đảo ta có KI // BC.
Hot: 1000+ Đề thi giữa kì 1 file word cấu trúc mới 2025 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Nhắn tin Zalo