Đề thi Học kì 2 Toán lớp 8 cực hay, có đáp án (Tự Luận - Đề 1)
35 người thi tuần này 5.0 6.7 K lượt thi 4 câu hỏi 90 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Bộ 10 đề thi cuối kì 2 Toán 8 Kết nối tri thức có đáp án - Đề 10
Bộ 10 đề thi cuối kì 2 Toán 8 Kết nối tri thức có đáp án - Đề 9
Bộ 10 đề thi giữa kì 2 Toán 8 Chân trời sáng tạo có đáp án - Đề 10
Bộ 10 đề thi giữa kì 2 Toán 8 Chân trời sáng tạo có đáp án - Đề 09
Bộ 10 đề thi giữa kì 2 Toán 8 Chân trời sáng tạo có đáp án - Đề 08
Bộ 10 đề thi giữa kì 2 Toán 8 Chân trời sáng tạo có đáp án - Đề 07
Bộ 10 đề thi giữa kì 2 Toán 8 Chân trời sáng tạo có đáp án - Đề 06
Bộ 10 đề thi giữa kì 2 Toán 8 Chân trời sáng tạo có đáp án - Đề 05
Danh sách câu hỏi:
Lời giải
a) Điều kiện: x + 2 ≠ 0 và x – 2 ≠ 0 ⇔ x ≠ ± 2
(Khi đó: x2 – 4 = (x + 2)(x – 2) ≠ 0)
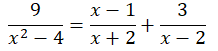
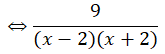
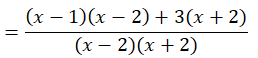
![]()
![]()
Vậy tập nghiệm của pt là: S = {-1; 1}
b) Điều kiện: 2x ≥ 0 ⇔ x ≥ 0
Khi đó: |x – 5| = 2x ⇔ x – 5 = 2x hoặc x – 5 = -2x
⇔ x = -5 hoặc x = 5/3
Vì x ≥ 0 nên ta lấy x = 5/3 . Tập nghiệm : S = {5/3}
c) x – 2)2 + 2(x – 1) ≤ x2 + 4
⇔ x2 – 4x + 4 + 2x – 2 ≤ x2 + 4
⇔ -2x ≤ 2
⇔ x ≥ -1
Tập nghiệm S = {x | x ≥ -1}
Lời giải
Gọi x (km) là quãng đường AB (x > 0)
Thời gian đi từ A đến B là: x/60 (giờ)
Thời gian đi từ B về A là: x/45 (giờ)
Theo đề ra, ta có phương trình:
⇔ 3x + 4x = 7.180 ⇔ 7x = 7.180 ⇔ x = 180 (nhận)
Trả lời: Quãng đường AB dài 180km.
Lời giải
Ta có: a + b = 1 ⇔ b = 1 – a
Thay vào bất đẳng thức a2 + b2 ≥ 1/2 , ta được:
a2 + (1 – a)2 ≥ 1/2 ⇔ a2 + 1 – 2a + a2 ≥ 1/2
⇔ 2a2 – 2a + 1 ≥ 1/2 ⇔ 4a2 – 4a + 2 ≥ 1
⇔ 4a2 – 4a + 1 ≥ 0 ⇔ (2a – 1)2 ≥ 0 (luôn đúng)
Vậy bất đẳng thức được chứng minh
Lời giải
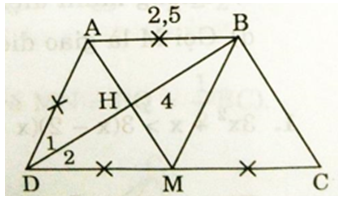
a) Ta có: AB = AD = CD/2 và M là trung điểm của CD (gt)
⇔ AB = DM và AB // DM
Do đó tứ giác ABMD là hình bình hành có AB = AD. Vậy ABMD là hình thoi.
b) M là trung điểm của CD nên BM là trung tuyến của ΔBDC mà MB = MD = MC. Do đó ΔBDC là tam giác vuông tại B hay DB ⊥ BC
c) ABMD là hình thoi (cmt) ⇔ ∠D1 = ∠D2
Do đó hai tam giác vuông AHD và CBD đồng dạng (g.g)
d) Ta có :
![]()
Xét tam giác vuông AHB, ta có :
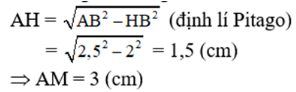
Dễ thấy tứ giác ABCM là hình bình hành (AB // CM và AB = CM)
⇒ BC = AM = 3 (cm)
Ta có:
![]()
M là trung điểm của DC nên
SBMD = SBMC = SBCD/2 = 3 (cm2) (chung đường cao kẻ từ B và MD = MC)
Mặt khác ΔABD = ΔMDB (ABCD là hình thoi)
⇔ SABD = SBMD = 3 (cm2)
Vậy SABCD = SABD + SBMD + SBMC = 9 (cm2)