Thi Online Bài tập Toán 8 Chủ đề 11: Hình chữ nhật có đáp án
Dạng 1: Chứng minh tứ giác là hình chữ nhật có đáp án
-
1556 lượt thi
-
6 câu hỏi
-
45 phút
Câu 1:
Cho tứ giác ABCD có hai đường chéo vuông góc với nhau. Gọi E, F, G, H theo thứ tự là trung điểm của các cạnh AB, BC, CD, DA
a) Chứng minh EFGH là hình bình hành.
Cho tứ giác ABCD có hai đường chéo vuông góc với nhau. Gọi E, F, G, H theo thứ tự là trung điểm của các cạnh AB, BC, CD, DA
a) Chứng minh EFGH là hình bình hành.
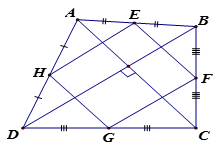
a) Ta có: là đường trung bình của và (1)
Ta có: là đường trung bình của và (2)
Từ (1), (2) suy ra EF // HG và EF = HG
Vậy EFGH là hình bình hành (3)
Câu 2:
b) Tứ giác EFGH là hình gì?
b) Ta có: EFGH là hình bình hành.
Ta có: là đường trung bình của
Ta có:
Ta có: (4)
Từ (3), (4), suy ra hình bình hành EFGH có nên EFGH là hình chữ nhật.
Câu 3:
Cho tam giác ABC vuông cân tại C. Trên các cạnh AC, BC lần lượt lấy các điểm P, Q sao cho AP = CQ. Từ điểm P vẽ PM song song với
a) Chứng minh PM = CQ.
Cho tam giác ABC vuông cân tại C. Trên các cạnh AC, BC lần lượt lấy các điểm P, Q sao cho AP = CQ. Từ điểm P vẽ PM song song với
a) Chứng minh PM = CQ.
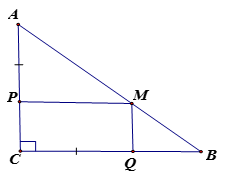
a) Ta có: ( vì vuông cân tại C ) (1)
Vì PM // BC nên ( hai góc đồng vị) (2)
Từ (1), (2) suy ra ( vì cùng bằng )
cân tại P => AP = PM ( hai cạnh bên bằng nhau)
Ta có:
Câu 4:
b) Chứng minh tứ giác PCQM là hình chữ nhật.
b) Ta có: là hình bình hành ( tứ giác có một cặp cạnh đối song song và bằng nhau)
Lại có
Vậy PCQM là hình chữ nhật.
Câu 5:
Cho tam giác ABC, các trung tuyến BM và CN cắt nhau tại G. Gọi P là điểm đối xứng của M qua G, gọi Q là điểm đối xứng của N qua G.
a) Tứ giác MNPQ là hình gì? Vì sao?
Cho tam giác ABC, các trung tuyến BM và CN cắt nhau tại G. Gọi P là điểm đối xứng của M qua G, gọi Q là điểm đối xứng của N qua G.
a) Tứ giác MNPQ là hình gì? Vì sao?
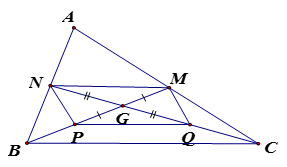
a) Ta có:
GM = GP (vì P là điểm đối xứng của M qua G) (1)
GN = GQ ( vì Q là điểm đối xứng của N qua G) (2)
Từ (1), (2) suy ra MNPQ là hình bình hành ( vì có G là trung điểm của hai đường chéo MP và NQ )
Bài thi liên quan:
Dạng 4: Tìm điều kiện để tứ giác là hình chữ nhật có đáp án
3 câu hỏi 45 phút
Dạng 5: Bài nâng cao và phát triển tư duy có đáp án
13 câu hỏi 45 phút
Dạng 6: Bài tập tự luyện (Phiếu số 1)
22 câu hỏi 45 phút
Dạng 7: Bài tập tự luyện (Phiếu số 2)
24 câu hỏi 45 phút
Các bài thi hot trong chương:
( 1 K lượt thi )
( 893 lượt thi )
( 1 K lượt thi )
( 583 lượt thi )
( 2 K lượt thi )
( 1.8 K lượt thi )
( 1.7 K lượt thi )
( 1.7 K lượt thi )
( 1.3 K lượt thi )
Đánh giá trung bình
0%
0%
0%
0%
0%