Dạng 1. Dùng dấu hiệu nhận biết để chứng minh một tứ giác là hình thoi có đáp án
31 người thi tuần này 4.6 2.3 K lượt thi 5 câu hỏi 45 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Bộ 10 đề thi cuối kì 2 Toán 8 Kết nối tri thức có đáp án - Đề 10
Bộ 10 đề thi cuối kì 2 Toán 8 Kết nối tri thức có đáp án - Đề 9
Bộ 10 đề thi giữa kì 2 Toán 8 Chân trời sáng tạo có đáp án - Đề 10
Bộ 10 đề thi giữa kì 2 Toán 8 Chân trời sáng tạo có đáp án - Đề 09
Bộ 10 đề thi giữa kì 2 Toán 8 Chân trời sáng tạo có đáp án - Đề 08
Bộ 10 đề thi giữa kì 2 Toán 8 Chân trời sáng tạo có đáp án - Đề 07
Bộ 10 đề thi giữa kì 2 Toán 8 Chân trời sáng tạo có đáp án - Đề 06
Bộ 10 đề thi giữa kì 2 Toán 8 Chân trời sáng tạo có đáp án - Đề 05
Danh sách câu hỏi:
Lời giải
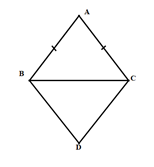
Xét tứ giác ABDC có:
AB // CD; AC // BD (gt)
=> tứ giác ABDC là hình bình hành.
Lại có: AB = AC ( cân tại A )
Nên tứ giác ABDC là hình thoi. (đpcm)
Lời giải
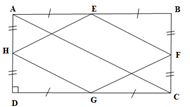
Vì E, F lần lượt là trung điểm của AB, BC nên:
EFlà đường trung bình của . Do đó:
Vì G, H lần lượt là trung điểm của CD, DA nên:
GH là đường trung bình của . Do đó:
Từ (1) và (2) suy ra:
Vậy tứ giác EFGH là hình bình hành
Xét và có:
EA = EB (Giả thiết)
AH = BF (Vì AD = BC)
Suy ra:
=> HE = FE (**)
Từ (*) và (**) ta được tứ giác là hình thoi (đpcm).
Lời giải
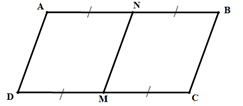
Hình bình hành ABCD có M, N lần lượt là trung điểm AB, CD nên:
Do đó tứ giác ANMD là hình bình hành (*)
Ta có: AB = 2.AD (giả thiết)
N là trung điểm AB nên AB = 2.AN
Nên AD = AN
Từ (*) và (**) ta được tứ giác ANMD là hình thoi. (đpcm).
Lời giải
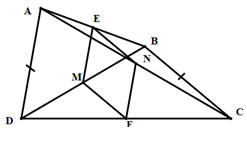
Vì E, M lần lượt là trung điểm của AB, BD nên:
EM là đường trung bình của .
Do đó:
Vì N, F lần lượt là trung điểm của AC, DC nên:
NF là đường trung bình của ACD . Do đó:
Từ (1), (2) suy ra EMFN là hình bình hành. (*)
Vì E, N lần lượt là trung điểm của AB, AC nên:
EN là đường trung bình của ABC . Do đó:
Mà AD = BC (giả thiết) (4)
Từ (1), (3), (4) ta được: EM = EN (**)
Từ (*) và (**) ta được tứ giác EMFNlà hình thoi. (đpcm).
Lời giải
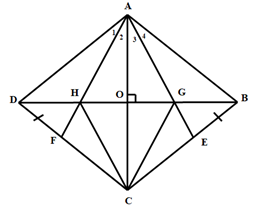
Gọi O là giao điểm của AC và BD khi đó (Vì O là giao điểm của hai đường chéo của hình thoi)
Xét và có:
AB = AD (Vì ABCD là hình thoi)
(Vì ABCD là hình thoi)
BE = DF (giả thiết)
Suy ra
Suy ra (hai góc tương ứng).
Mà AC là phân giác của
Do đó AO là phân giác của (*)
Xét có:
AO là đường cao, đồng thời là đường phân giác nên cân tại A.
Suy ra HO = OG (1)
Lại có AO = OC ( Vì ABCD là hình thoi có trung điểm O ) (2)
Từ (1) và (2) suy ra AGCH là hình bình hành. (**)
Từ (*) và (**) ta được tứ giác AGCH là hình thoi. (đpcm)