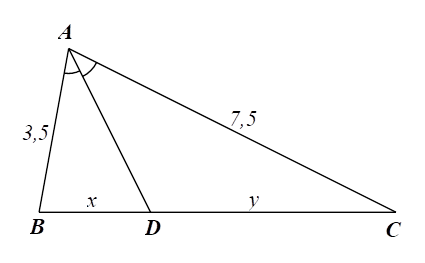Bộ 10 đề thi giữa kì 2 Toán 8 Chân trời sáng tạo có đáp án - Đề 09
79 người thi tuần này 4.6 1.1 K lượt thi 9 câu hỏi 90 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Bộ 10 đề thi cuối kì 2 Toán 8 Cánh diều có đáp án - Đề 10
Bộ 10 đề thi cuối kì 2 Toán 8 Cánh diều có đáp án - Đề 09
Bộ 10 đề thi cuối kì 2 Toán 8 Cánh diều có đáp án - Đề 08
Bộ 10 đề thi cuối kì 2 Toán 8 Cánh diều có đáp án - Đề 07
Bộ 10 đề thi cuối kì 2 Toán 8 Cánh diều có đáp án - Đề 06
Bộ 10 đề thi cuối kì 2 Toán 8 Cánh diều có đáp án - Đề 05
Bộ 10 đề thi cuối kì 2 Toán 8 Cánh diều có đáp án - Đề 04
Bộ 10 đề thi cuối kì 2 Toán 8 Cánh diều có đáp án - Đề 03
Danh sách câu hỏi:
Câu 1
Lời giải
Hướng dẫn giải
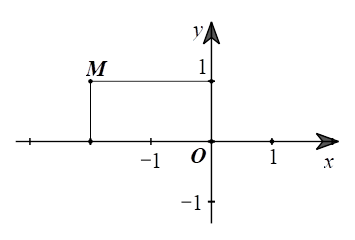
Đáp án đúng là: C
Điểm \(M\) có hoành độ là \( - 2\) và tung độ là \(1\) nên có tọa độ được viết là \(M\left( { - 2;1} \right).\)
Câu 2
Lời giải
Hướng dẫn giải
Đáp án đúng là: B
Ta có \(y = \frac{{1 - 4x}}{2} = \frac{1}{2} - 2x = - 2x + \frac{1}{2}.\)
Do đó hệ số góc của đường thẳng đã cho là \( - 2.\)
Câu 3
Lời giải
Hướng dẫn giải
Đáp án đúng là: A
Xét hàm số \(y = - \frac{1}{2}x + 1.\)
⦁ Thay \(x = 1\) vào hàm số ta được \(y = - \frac{1}{2} \cdot 1 + 1 = \frac{1}{2}.\)
Do đó đồ thị hàm số đi qua điểm \(\left( {1;\frac{1}{2}} \right).\)
⦁ Thay \(x = 3\) vào hàm số ta được \(y = - \frac{1}{2} \cdot 3 + 1 = - \frac{1}{2}.\)
Do đó đồ thị hàm số đi qua điểm \(\left( {3; - \frac{1}{2}} \right).\)
⦁ Thay \(x = - 1\) vào hàm số ta được \(y = - \frac{1}{2} \cdot \left( { - 1} \right) + 1 = \frac{3}{2}.\)
Do đó đồ thị hàm số đi qua điểm \(\left( { - 1;\frac{3}{2}} \right).\)
⦁ Thay \(x = - 2\) vào hàm số ta được \(y = - \frac{1}{2} \cdot \left( { - 2} \right) + 1 = 2.\)
Do đó đồ thị hàm số đi qua điểm \(\left( { - 2;2} \right).\)
Vậy ta chọn phương án A.Câu 4
C. \(\frac{{DE}}{{AC}} = \frac{{BC}}{{BE}}.\)
Lời giải
Hướng dẫn giải
Đáp án đúng là: D
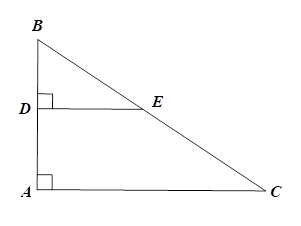
Vì \(DE \bot AB\) và \(AC \bot AB\) nên \(DE\,{\rm{//}}\,AC.\)
Xét \(\Delta ABC\) có \(DE\,{\rm{//}}\,AC,\) theo định lí Thalès ta có: \(\frac{{BD}}{{AD}} = \frac{{BE}}{{EC}}.\)Câu 5
Lời giải
Hướng dẫn giải
Đáp án đúng là: A
Xét \(\Delta ABC\) có \(AD\) là tia phân giác \(\widehat {BAC}\) (do \(\widehat {BAD} = \widehat {CAD})\) nên ta có:
\(\frac{{DB}}{{DC}} = \frac{{AB}}{{AC}} = \frac{{3,5}}{{7,5}} = \frac{7}{{15}}\) (tính chất đường phân giác).
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.