20 câu trắc nghiệm Toán 8 Chân trời sáng tạo Ôn tập chương 7 (Đúng sai - Trả lời ngắn) có đáp án
70 người thi tuần này 4.6 190 lượt thi 20 câu hỏi 45 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Bộ 10 đề thi cuối kì 2 Toán 8 Cánh diều có đáp án - Đề 10
Bộ 10 đề thi cuối kì 2 Toán 8 Cánh diều có đáp án - Đề 09
Bộ 10 đề thi cuối kì 2 Toán 8 Cánh diều có đáp án - Đề 08
Bộ 10 đề thi cuối kì 2 Toán 8 Cánh diều có đáp án - Đề 07
Bộ 10 đề thi cuối kì 2 Toán 8 Cánh diều có đáp án - Đề 06
Bộ 10 đề thi cuối kì 2 Toán 8 Cánh diều có đáp án - Đề 05
Bộ 10 đề thi cuối kì 2 Toán 8 Cánh diều có đáp án - Đề 04
Bộ 10 đề thi cuối kì 2 Toán 8 Cánh diều có đáp án - Đề 03
Danh sách câu hỏi:
Câu 1
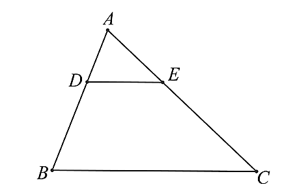
A. \(\frac{{AD}}{{AB}} = \frac{{AE}}{{AC}}\) suy ra \(DE\parallel BC\).
A. \(\frac{{AD}}{{AB}} = \frac{{AE}}{{AC}}\) suy ra \(DE\parallel BC\).
C. \(\frac{{AB}}{{DB}} = \frac{{AC}}{{EC}}\) suy ra \(DE\parallel BC\).
D. \(\frac{{AD}}{{DE}} = \frac{{AE}}{{BC}}\) suy ra \(DE\parallel BC\).
Lời giải
Đáp án đúng là: D
Nếu ta có tỉ số \(\frac{{AD}}{{AB}} = \frac{{AE}}{{AC}}\), \(\frac{{AD}}{{DB}} = \frac{{AE}}{{EC}}\), \(\frac{{AB}}{{DB}} = \frac{{AC}}{{EC}}\) thì suy ra \(DE\parallel BC\).
Câu 2
A. Đường trung bình của tam giác là đoạn thẳng nối chân đường cao của tam giác.
B. Đường trung bình của tam giác là đoạn nối trung điểm hai cạnh của tam giác.
C. Trong một tam giác chỉ có một đường trung bình.
D. Đường trung bình của tam giác là đường nối từ một đỉnh đến trung điểm cạnh đối diện.
Lời giải
Đáp án đúng là: B
Đường trung bình của tam giác là đoạn nối trung điểm hai cạnh của tam giác.
Câu 3
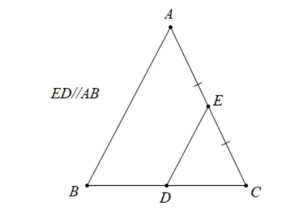
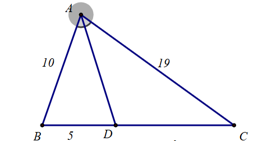
A. \(AE = \frac{1}{2}BC.\)
B. \(D\) là trung điểm của \(BC.\)
C. \(DE\) không song song với \(AB.\)
D. \(DB > DC.\)
Lời giải
Đáp án đúng là: B
Từ hình vẽ, ta có \(ED\parallel AB\) và \(E\) là trung điểm \(AC\) nên \(DE\) là đường trung bình của \(\Delta ABC\).
Do đó, \(D\) là trung điểm của \(BC.\)
Lời giải
Đáp án đúng là: C
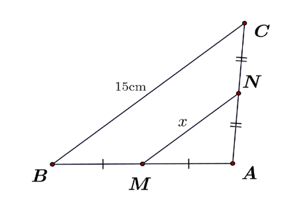
Nhận thấy, \(MN\) là đường trung bình của tam giác \(ABC\).
Do đó, \(MN = \frac{1}{2}BC = \frac{1}{2} \cdot 15 = 7,5{\rm{ }}\left( {{\rm{cm}}} \right)\).
Câu 5
Lời giải
Đáp án đúng là: B
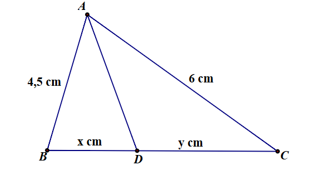
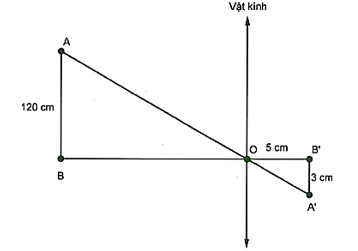
Ta có: \(\frac{{AB}}{{CD}} = \frac{4}{{20}} = \frac{1}{5}.\)
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 8
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 9
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 10
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 11
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 12
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 13
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 14
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 15
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.