10 Bài tập Tính độ dài đoạn thẳng bằng cách sử dụng tính chất đường trung bình (có lời giải)

Đáp án đúng là: B

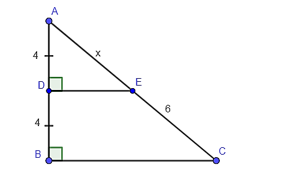
Ta có DE ⊥ AB, BC ⊥ AB, suy ra DE // BC.

Trong tam giác ABC có D là trung điểm AB (do AD = DB = 4), DE // BC.

Do đó E là trung điểm của AC (tính chất đường trung bình của tam giác).

Suy ra AE = EC = 6. Vậy x = 6.

Đáp án đúng là: C

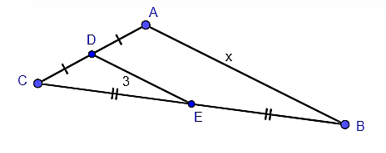
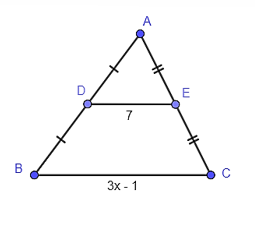
Trong tam giác ABC có D là trung điểm của AC, E là trung điểm của BC.

Do đó DE là đường trung bình của tam giác ABC.

Suy ra $\text{DE}=\frac{1}{2}\text{AB}$(tính chất đường trung bình của tam giác).

 Hay AB = 2DE = 2 ⋅ 3 = 6.

Vậy AB = 6.

Đáp án đúng là: C

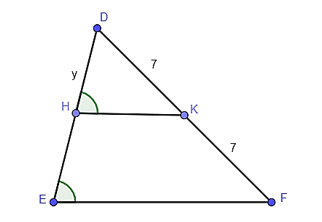
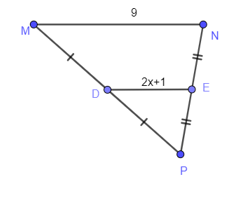
Ta có DK = KF = 7 (cm), suy ra K là trung điểm của DF.

Lại có $\widehat{\text{DHK}}=\widehat{\text{DEF}}$  mà hai góc này ở vị trí đồng vị nên HK // EF.

Trong tam giác DEF có K là trung điểm của DF, HK // EF.

Do đó H là trung điểm của DE (tính chất đường trung bình của tam giác).

Suy ra $\text{DH}=\frac{1}{2}\text{DE}=\frac{1}{2}\cdot 13=6,5$  (cm). Vậy y = 6,5 cm.

Đáp án đúng là: A

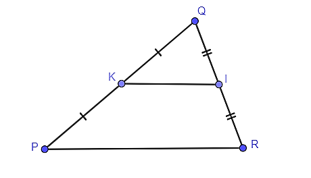
Trong tam giác PQR có I là trung điểm của QR, K là trung điểm QP.

Do đó IK là đường trung bình của tam giác PQR.

Suy ra  $\text{IK}=\frac{1}{2}\text{PR }$và IK // PR (tính chất đường trung bình của tam giác).

Vậy A đúng.

Đáp án đúng là: D

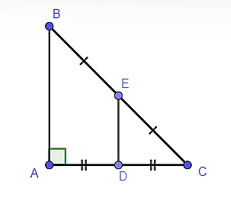
Trong tam giác ABC có D là trung điểm của AC, E là trung điểm BC.

Do đó DE là đường trung bình của tam giác ABC.

Suy ra $\text{DE}=\frac{1}{2}\text{AB}$  (tính chất đường trung bình của tam giác).

Hay AB = 2DE = 2 ⋅ 5 = 10 (cm).

Vì tam giác ABC vuông cân tại A nên AC = AB = 10 cm.

Đáp án đúng là: C

Trong tam giác DEF có H là trung điểm của DE, I là trung điểm EF.

Do đó HI là đường trung bình của tam giác DEF.

Suy ra  $\text{HI}=\frac{1}{2}\text{DF\hspace{0.17em}=}\frac{1}{2}\cdot 14=7$(cm) (tính chất đường trung bình của tam giác).

Lại có H là trung điểm DE nên  $\text{HE}=\frac{1}{2}\text{DE}=\frac{1}{2}\cdot 8=4$(cm).

x + y = HE + HI = 4 + 7 = 11 (cm).

Đáp án đúng là: A

Trong tam giác MNP có D là trung điểm của MP, E là trung điểm NP.

Do đó DE là đường trung bình của tam giác MNP.

Suy ra  $\text{DE}=\frac{1}{2}\text{MN=}\frac{1}{2}\cdot 9=4,5$(tính chất đường trung bình của tam giác).

Theo đề bài ta có DE = 2x + 1 nên 2x + 1 = 4,5.

Suy ra 2x = 3,5.

Vậy x = 1,75.

Đáp án đúng là: B

Trong tam giác ABC có D là trung điểm của AB, E là trung điểm BC.

Do đó DE là đường trung bình của tam giác ABC.

Suy ra  $\text{DE}=\frac{1}{2}\text{AC}$(tính chất đường trung bình của tam giác).

Hay AC = 2DE = 2 ⋅ 6 = 12 (cm).

Diện tích tam giác ABC là:

$\frac{1}{2}\cdot \text{BH}\cdot \text{AC}=\frac{1}{2}\cdot 5\cdot 12=30$ (cm²).

Đáp án đúng là: C

Vì tam giác ABC cân tại A nên AC = AB = 3 cm.

Lại có $\text{BM}=\frac{1}{2}\text{AB}=\frac{1}{2}\cdot 3=1,5\text{\hspace{0.17em}\hspace{0.17em}(cm)};\text{NC}=\frac{1}{2}\text{AC}=\frac{1}{2}\cdot 3=1,5\text{\hspace{0.17em}\hspace{0.17em}(cm)}$  (do M, N lần lượt là trung điểm của AB, AC).

Trong tam giác ABC có M là trung điểm của AB, N là trung điểm AC.

Do đó MN là đường trung bình của tam giác ABC.

Suy ra  $\text{MN}=\frac{1}{2}\text{BC=}\frac{1}{2}\cdot 4=2$(cm) (tính chất đường trung bình của tam giác).

Chu vi tứ giác BMNC là:

BM + MN + NC + BC = 1,5 + 2 + 1,5 + 4 = 9 (cm).

Đáp án đúng là: C

Trong tam giác ABC có D là trung điểm của AB, E là trung điểm AC.

Do đó DE là đường trung bình của tam giác ABC.

Suy ra $\text{DE}=\frac{1}{2}\text{BC}$  (tính chất đường trung bình của tam giác).

Hay BC = 2DE = 2 ⋅ 7 = 14.

Mà BC = 3x – 1 nên 3x – 1 = 14, suy ra 3x = 15.

Vậy x = 5.