Người ta dùng máy ảnh để chụp vật \(AB\) cao 120 cm (như hình vẽ). Sau khi tráng phim thấy ảnh cao 3 cm. Biết khoảng cách từ phim đến vật kính của máy ảnh lúc chụp là \(5{\rm{ cm}}{\rm{.}}\)
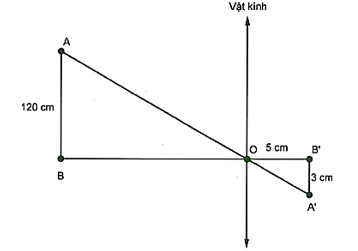
Hỏi vật \(AB\) được đặt cách vật kính máy ảnh là bao nhiêu mét?
Quảng cáo
Trả lời:
Đáp án: 200
Xét \(\Delta OAB\) có \(AB\parallel A'B'\) (gt) nên: \(\frac{{OB'}}{{OB}} = \frac{{A'B'}}{{AB}}\) (hệ quả định lí Thalès).
Suy ra \(\frac{5}{{OB}} = \frac{3}{{120}}\) nên \(OB = \frac{{120 \cdot 5}}{3} = 200{\rm{ }}\left( {\rm{m}} \right)\).
Vậy vật \(AB\) được đặt cách vật kính máy ảnh là 200 m.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đáp án: 37,3
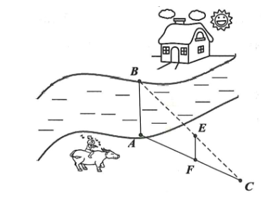
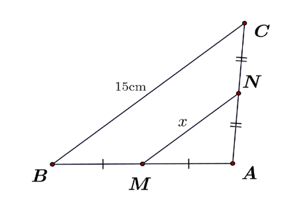
Xét \(\Delta ABC\) có \(FE\parallel BA\) (gt) nên \(\frac{{CF}}{{CA}} = \frac{{EF}}{{AB}}\) (hệ quả định lí Thalès).
Suy ra \(\frac{{44,2}}{{44,5 + 44,2}} = \frac{{18,6}}{{AB}}\) suy ra \(AB = \frac{{18,6 \cdot 88,7}}{{44,2}} = 37,3{\rm{ }}\left( {\rm{m}} \right)\).
Vậy chiều rộng của khúc sông \(AB\) là \(37,3{\rm{ m}}{\rm{.}}\)
Câu 2
Lời giải
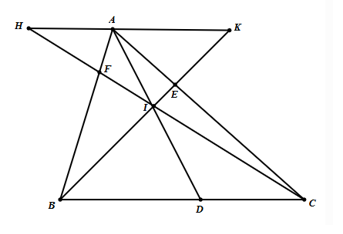
a) Đúng.
Vì \(AK\parallel BD\) nên áp dụng định lí Thalès, ta có: \(\frac{{AI}}{{ID}} = \frac{{AK}}{{BD}}.\) (1)
Vì \(AH\parallel DC\) nên suy ra \(\frac{{AI}}{{ID}} = \frac{{AH}}{{DC}}\) (2)
Từ (1) và (2) suy ra \(\frac{{AK}}{{BD}} = \frac{{AH}}{{DC}}\).
b) Đúng.
Ta có \(\frac{{AF}}{{BF}} = \frac{{AH}}{{BC}}{\rm{ }}\left( {AH\parallel BC} \right)\) và \(\frac{{AE}}{{CE}} = \frac{{AK}}{{BC}}{\rm{ }}\left( {AK\parallel BC} \right)\).
Do đó, \(\frac{{AF}}{{BF}} + \frac{{AE}}{{CE}} = \frac{{AH}}{{BC}} + \frac{{AK}}{{BC}} = \frac{{HK}}{{BC}}.\)
c) Đúng.
Lại có \(\frac{{HK}}{{BC}} = \frac{{HI}}{{IC}}{\rm{ }}\left( {HK\parallel BC} \right)\) và \(\frac{{HI}}{{IC}} = \frac{{AI}}{{ID}}{\rm{ }}\left( {AH\parallel BC} \right)\).
Từ đây suy ra \(\frac{{AF}}{{BF}} + \frac{{AE}}{{CE}} = \frac{{HK}}{{BC}} = \frac{{HI}}{{IC}} = \frac{{AI}}{{ID}}\).
Suy ra \(\frac{{AE}}{{CE}} + \frac{{AF}}{{BF}} = \frac{{AI}}{{ID}}\).
d) Sai.
Từ phần a), ta có: \(\frac{{AK}}{{BD}} = \frac{{AH}}{{DC}}\) suy ra \(\frac{{BD}}{{DC}} = \frac{{AK}}{{AH}}\).
Lại có \(AK\parallel BC\) suy ra \(\frac{{EC}}{{EA}} = \frac{{BC}}{{AK}}\).
Mặt khác \(AH\parallel BC\) nên \(\frac{{FA}}{{FB}} = \frac{{HA}}{{BC}}\).
Từ đây suy ra
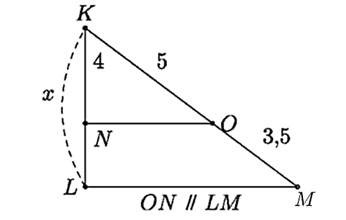
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
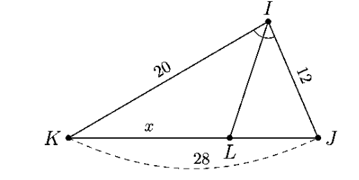
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.