Bộ 10 đề thi giữa kì 2 Toán 8 Chân trời sáng tạo có đáp án - Đề 07
34 người thi tuần này 4.6 2 K lượt thi 9 câu hỏi 90 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Bài tập Tính diện tích xung quanh và thể tích của hình chóp tứ giác đều lớp 8 (có lời giải)
Bài tập Tính diện tích xung quanh và thể tích của hình chóp tam giác đều lớp 8 (có lời giải)
Bài tập Các bài toán thực tiễn gắn với việc vận dụng các tam giác vuông đồng dạng lớp 8 (có lời giải)
Bài tập Các bài toán thực tiễn gắn với việc vận dụng định lí Pythagore lớp 8 (có lời giải)
Bài tập Chứng minh các tính chất hình học lớp 8 (có lời giải)
Bài tập Tính độ dài cạnh trong tam giác vuông bằng cách sử dụng định lí Pythagore lớp 8 (có lời giải)
Danh sách câu hỏi:
Câu 1/9
Lời giải
Hướng dẫn giải
Đáp án đúng là: A
Vì đồ thị hàm số \(y = ax + 3\) đi qua điểm \[\left( {1;5} \right)\] nên ta có:
\(5 = a \cdot 1 + 3\)
Suy ra \(a = 2.\) Khi đó ta có hàm số \(y = 2x + 3.\)
Đồ thị hàm số \(y = 2x + 3\) đi qua điểm có hoành độ bằng \( - 5\) nên ta có tung độ của điểm này là:
\(y = 2 \cdot \left( { - 5} \right) + 3 = - 10 + 3 = - 7.\)
Vậy ta chọn phương án A.
Câu 2/9
Lời giải
Hướng dẫn giải
Đáp án đúng là: B
Hàm số bậc nhất có dạng \(y = ax + b\) với \(a \ne 0.\)
Hàm số \[y = 2 - \frac{{4x}}{3} = - \frac{4}{3}x + 2\] có dạng trên nên là hàm số bậc nhất.
Câu 3/9
Lời giải
Hướng dẫn giải
Đáp án đúng là: C
Ta có hệ số góc của đường thẳng \(y = - 2x + 1\) là \(a = - 2 < 0.\)
Do đó góc tạo bởi đường thẳng \(y = - 2x + 1\) với trục \(Ox\) là góc tù.Câu 4/9
Lời giải
Hướng dẫn giải
Đáp án đúng là: A
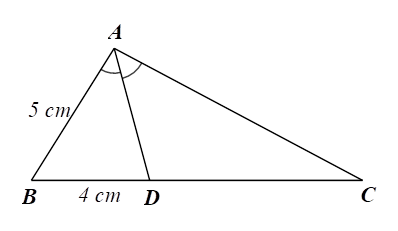
Xét \(\Delta ABC\) có \(AD\) là đường phân giác của góc \(BAC\) (do \(\widehat {BAD} = \widehat {CAD}),\) nên \(\frac{{AB}}{{AC}} = \frac{{DB}}{{DC}}\) (tính chất đường phân giác).
Suy ra \(\frac{{AB}}{{DB}} = \frac{{AC}}{{DC}}\) (tính chất tỉ lệ thức)
Do đó \(\frac{{AC}}{{CD}} = \frac{5}{4}.\)Câu 5/9
Lời giải
Hướng dẫn giải
Đáp án đúng là: D
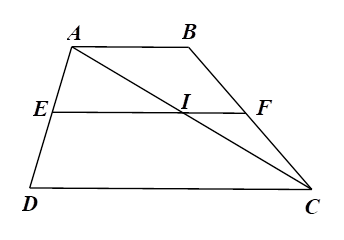
Xét \(\Delta ADC\) với \(EI\,{\rm{//}}\,DC\) ta có:
⦁ \(\frac{{AE}}{{ED}} = \frac{{AI}}{{IC}}\) (định lí Thalès). Do đó A là khẳng định đúng.
⦁ \(\frac{{AI}}{{AC}} = \frac{{EI}}{{DC}}\) (hệ quả của định lí Thalès). Do đó C là khẳng định đúng.
Xét \(\Delta ABC\) với \(IF\,{\rm{//}}\,AB\) ta có:
⦁ \(\frac{{AI}}{{IC}} = \frac{{BF}}{{FC}}\) (định lí Thalès).
Mà \(\frac{{AE}}{{ED}} = \frac{{AI}}{{IC}}\) nên \(\frac{{AE}}{{ED}} = \frac{{BF}}{{FC}}.\) Do đó A là khẳng định đúng.
⦁ \(\frac{{IC}}{{AC}} = \frac{{IF}}{{AB}}\) (hệ quả định lí Thalès). Do đó D là khẳng định sai.
Vậy ta chọn phương án D.
Câu 6/9
Lời giải
Hướng dẫn giải
Đáp án đúng là: C
Xét \[\Delta ABC\] vuông tại \(A,\) theo định lí Pythagore ta có: \(B{C^2} = A{B^2} + A{C^2} = {3^2} + {4^2} = 25.\)
Do đó \(BC = 5{\rm{\;cm}}.\)
Xét \[\Delta ABC\] có \(P,\,\,Q\) lần lượt là trung điểm của \(AB,\,\,AC\) nên \(PQ\) là đường trung bình của tam giác, do đó \(PQ = \frac{1}{2}BC = \frac{1}{2} \cdot 5 = 2,5{\rm{\;cm}}.\)Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 9/9
1) Tìm độ dài \[x\] trong mỗi trường hợp sau:
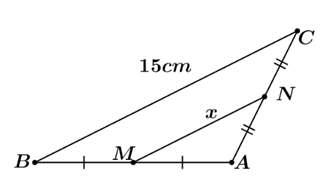
Hình 1
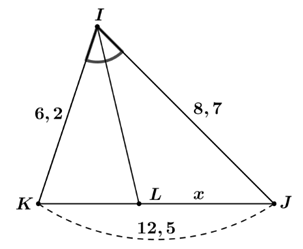
Hình 2
2) Cho hình thang \(ABCD\) có hai đáy \(AB\) và \(CD.\) Gọi \(M\) là trung điểm của \(CD,\) \(E\) là giao điểm của \(MA\) và \(BD,\) \(F\) là giao điểm của \(MB\) và \(AC.\)
a) Chứng minh rằng \[EF\,{\rm{//}}\,AB.\]
b) Đường thẳng \(EF\) cắt \(AD,\,\,BC\) lần lượt tại \(H\) và \(N.\)
i) Chứng minh \(HE = EF = FN.\)
ii) Biết \(AB = 7,5{\rm{\;cm}},\,\,CD = 12{\rm{\;cm}}.\) Tính độ dài \(HN.\)
1) Tìm độ dài \[x\] trong mỗi trường hợp sau:
|
Hình 1 |
Hình 2 |
2) Cho hình thang \(ABCD\) có hai đáy \(AB\) và \(CD.\) Gọi \(M\) là trung điểm của \(CD,\) \(E\) là giao điểm của \(MA\) và \(BD,\) \(F\) là giao điểm của \(MB\) và \(AC.\)
a) Chứng minh rằng \[EF\,{\rm{//}}\,AB.\]
b) Đường thẳng \(EF\) cắt \(AD,\,\,BC\) lần lượt tại \(H\) và \(N.\)
i) Chứng minh \(HE = EF = FN.\)
ii) Biết \(AB = 7,5{\rm{\;cm}},\,\,CD = 12{\rm{\;cm}}.\) Tính độ dài \(HN.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Xem tiếp với tài khoản VIP
Còn 3/9 câu hỏi, đáp án và lời giải chi tiết.
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập