Bộ 10 đề thi giữa kì 2 Toán 8 Chân trời sáng tạo có đáp án - Đề 05
51 người thi tuần này 4.6 1.1 K lượt thi 11 câu hỏi 90 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Bộ 10 đề thi cuối kì 2 Toán 8 Cánh diều có đáp án - Đề 10
Bộ 10 đề thi cuối kì 2 Toán 8 Cánh diều có đáp án - Đề 09
Bộ 10 đề thi cuối kì 2 Toán 8 Cánh diều có đáp án - Đề 08
Bộ 10 đề thi cuối kì 2 Toán 8 Cánh diều có đáp án - Đề 07
Bộ 10 đề thi cuối kì 2 Toán 8 Cánh diều có đáp án - Đề 06
Bộ 10 đề thi cuối kì 2 Toán 8 Cánh diều có đáp án - Đề 05
Bộ 10 đề thi cuối kì 2 Toán 8 Cánh diều có đáp án - Đề 04
Bộ 10 đề thi cuối kì 2 Toán 8 Cánh diều có đáp án - Đề 03
Danh sách câu hỏi:
Câu 1
Lời giải
Hướng dẫn giải
Đáp án đúng là: D
Hàm số \(y = ax + b\) là hàm số bậc nhất khi \(a \ne 0.\)Câu 2
Cho điểm \(A\) và \(B\) trong mặt phẳng tọa độ \(Oxy\) như hình bên. Khẳng định nào sau đây là đúng?
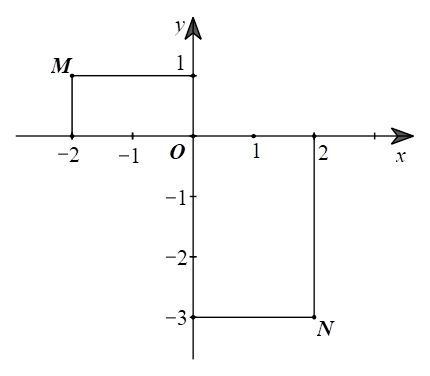
Cho điểm \(A\) và \(B\) trong mặt phẳng tọa độ \(Oxy\) như hình bên. Khẳng định nào sau đây là đúng?

Lời giải
Hướng dẫn giải
Đáp án đúng là: B
Trong hình vẽ trên,
⦁ điểm \(M\) có hoành độ là \[ - 2\] và tung độ là \(1\) nên có tọa độ là \(M\left( { - 2;1} \right).\)
⦁ điểm \(N\) có hoành độ là \[2\] và tung độ là \( - 3\) nên có tọa độ là \(N\left( {2; - 3} \right).\)
Vậy ta chọn phương án B.
Câu 3
Lời giải
Hướng dẫn giải
Đáp án đúng là: D
Hai đường thẳng \(d:y = ax + b\,\,\left( {a \ne 0} \right)\) và \[d':y = a'x + b'\,\,\left( {a' \ne 0} \right)\] cắt nhau khi và chỉ khi \(a = a'\) và \[b \ne b'.\]
Câu 4
Lời giải
Hướng dẫn giải
Đáp án đúng là: A
⦁ \[\left( {{d_m}} \right)\] cắt trục tung tại điểm \[A\] nên hoành độ của điểm \[A\] bằng 0.
Khi đó tung độ của điểm \[A\] là: \[{y_A} = m \cdot 0 + 2 = 2.\]
Do đó \[\left( {{d_m}} \right)\] cắt trục tung tại điểm 2 nên khẳng định A là đúng.
⦁ \[\left( {{d_m}} \right)\] cắt trục hoành tại điểm \[B\] nên tung độ của điểm \[B\] bằng 0.
Khi đó hoành độ của điểm \[B\] thỏa mãn: \[0 = m \cdot {x_B} + 2,\] suy ra \({x_B} = \frac{{ - 2}}{m}\) (với \[m \ne 0).\]
Do đó \[\left( {{d_m}} \right)\] cắt trục hoành tại điểm \(\frac{{ - 2}}{m}\) (với \[m \ne 0)\] nên khẳng định C là sai.
⦁ \[\left( {{d_m}} \right)\]có hệ số là \(m,\) tuy nhiên ta chưa xác định được \(m\) mang giá trị âm hay dương nên khẳng định B là sai. Từ đó khẳng định D cũng sai.
Vậy ta chọn phương án A.
Câu 5
Lời giải
Hướng dẫn giải
Đáp án đúng là: C
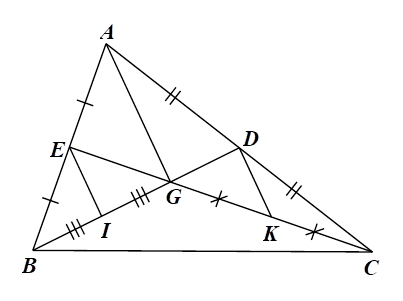
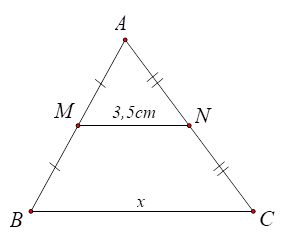
Xét \(\Delta ABG\) có \(E,\,\,I\) lần lượt là trung điểm của các cạnh \(AB,\,\,BG\) nên \(EI\) là đường trung bình của tam giác, do đó \(EI = \frac{1}{2}AG = \frac{1}{2} \cdot 4 = 2{\rm{\;cm}}.\)
Tương tự, \(DK\) là đường trung bình của \(\Delta ACG\) nên \(DK = \frac{1}{2}AG = \frac{1}{2} \cdot 4 = 2{\rm{\;cm}}.\)
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 8
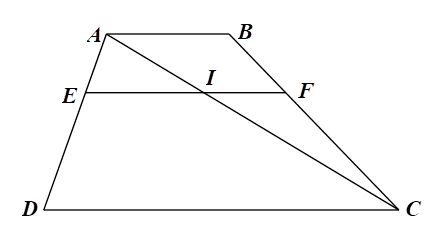
Cho hình vẽ bên, biết \[MN\,{\rm{//}}\,BC,\] \[NP\,{\rm{//}}\,AB\,.\]
Khẳng định nào sau đây là sai?
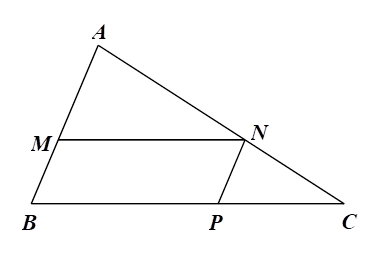
Cho hình vẽ bên, biết \[MN\,{\rm{//}}\,BC,\] \[NP\,{\rm{//}}\,AB\,.\]
Khẳng định nào sau đây là sai?

Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 11
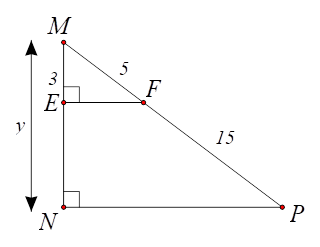
1) Tìm độ dài \[x,{\rm{ }}y\] trong mỗi trường hợp sau:
2) Cho tam giác \(ABC\) có \(AB = 4{\rm{\;cm}},\) \(AC = 5{\rm{\;cm}},\) \(BC = 6{\rm{\;cm}}.\) Các đường phân giác \(BD\) và \(CE\) cắt nhau tại \(I.\)
a) Tính \(AD,\,\,DC.\)
b) Tính các tỉ số \(\frac{{DI}}{{DB}},\,\,\frac{{BE}}{{BA}},\,\,\frac{{AD}}{{AC}}.\)
c) Tính tỉ số diện tích các tam giác \(DIE\) và \(ABC.\)
1) Tìm độ dài \[x,{\rm{ }}y\] trong mỗi trường hợp sau:
2) Cho tam giác \(ABC\) có \(AB = 4{\rm{\;cm}},\) \(AC = 5{\rm{\;cm}},\) \(BC = 6{\rm{\;cm}}.\) Các đường phân giác \(BD\) và \(CE\) cắt nhau tại \(I.\)
a) Tính \(AD,\,\,DC.\)
b) Tính các tỉ số \(\frac{{DI}}{{DB}},\,\,\frac{{BE}}{{BA}},\,\,\frac{{AD}}{{AC}}.\)
c) Tính tỉ số diện tích các tam giác \(DIE\) và \(ABC.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.