1) Tìm độ dài \[x,{\rm{ }}y\] trong mỗi trường hợp sau:
2) Cho tam giác \(ABC\) có \(AB = 4{\rm{\;cm}},\) \(AC = 5{\rm{\;cm}},\) \(BC = 6{\rm{\;cm}}.\) Các đường phân giác \(BD\) và \(CE\) cắt nhau tại \(I.\)
a) Tính \(AD,\,\,DC.\)
b) Tính các tỉ số \(\frac{{DI}}{{DB}},\,\,\frac{{BE}}{{BA}},\,\,\frac{{AD}}{{AC}}.\)
c) Tính tỉ số diện tích các tam giác \(DIE\) và \(ABC.\)
1) Tìm độ dài \[x,{\rm{ }}y\] trong mỗi trường hợp sau:
2) Cho tam giác \(ABC\) có \(AB = 4{\rm{\;cm}},\) \(AC = 5{\rm{\;cm}},\) \(BC = 6{\rm{\;cm}}.\) Các đường phân giác \(BD\) và \(CE\) cắt nhau tại \(I.\)
a) Tính \(AD,\,\,DC.\)
b) Tính các tỉ số \(\frac{{DI}}{{DB}},\,\,\frac{{BE}}{{BA}},\,\,\frac{{AD}}{{AC}}.\)
c) Tính tỉ số diện tích các tam giác \(DIE\) và \(ABC.\)
Câu hỏi trong đề: Bộ 10 đề thi giữa kì 2 Toán 8 Chân trời sáng tạo có đáp án !!
Quảng cáo
Trả lời:
|
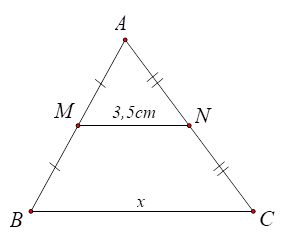
1) ⦁ Hình 1: Tam giác \[ABC\] có \[M,\,\,N\] lần lượt là trung điểm của \[AB\] và \[AC\] nên \[MN\] là đường trung bình của tam giác. Do đó \[MN = \frac{1}{2}BC.\] Suy ra \[x = BC = 2MN = 2 \cdot 3,5 = 7\left( {{\rm{cm}}} \right).\] Vậy \(x = 7{\rm{\;cm}}.\) |
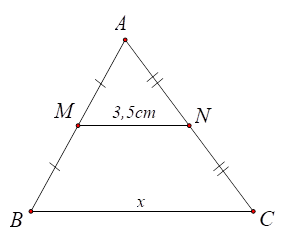 Hình 1 |
|
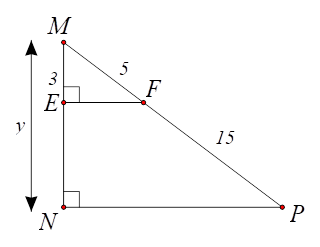
⦁ Hình 2: Ta có: \[EF \bot MN,\,\,NP \bot MN\] nên \[EF\,{\rm{//}}\,NP.\] \(MP = MF + FP = 5 + 15 = 20.\) Tam giác \[MNP\] có \[EF\,{\rm{//}}\,NP,\] theo định lí Thalès ta có: \[\frac{{ME}}{{MN}} = \frac{{MF}}{{MP}}\] hay \(\frac{3}{y} = \frac{5}{{20}},\) suy ra \(y = \frac{{3 \cdot 20}}{5} = 12.\) Vậy \(y = 12.\) |
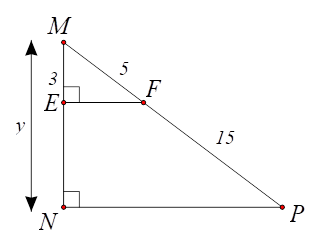 Hình 2 |
2)
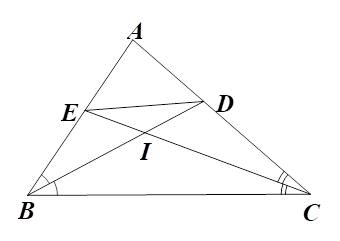
a) Xét \(\Delta ABC\) có \(BD\) là tia phân giác của \(\widehat {ABC}\) nên \[\frac{{BA}}{{BC}} = \frac{{DA}}{{DC}}\] (tính chất đường phân giác), do đó \[\frac{{DC}}{{BC}} = \frac{{DA}}{{BA}}.\]
Theo tính chất dãy tỉ số bằng nhau ta có \[\frac{{DC}}{{BC}} = \frac{{DA}}{{BA}} = \frac{{DC + DA}}{{BC + BA}} = \frac{{AC}}{{BC + BA}} = \frac{5}{{6 + 4}} = \frac{1}{2}.\]
Do đó \(AD = \frac{1}{2}AB = \frac{1}{2} \cdot 4 = 2{\rm{\;cm}};\) \(DC = \frac{1}{2}BC = \frac{1}{2} \cdot 6 = 3{\rm{\;cm}}.\)
b) Xét \(\Delta BCD\) có \(CI\) là tia phân giác của \(\widehat {DCB}\) nên \[\frac{{DI}}{{BI}} = \frac{{DC}}{{BC}} = \frac{1}{2}\] (tính chất đường phân giác), suy ra \[\frac{{DI}}{{BI + DI}} = \frac{1}{{2 + 1}},\] hay \(\frac{{DI}}{{DB}} = \frac{1}{3}.\)
Chứng minh tương tự, ta cũng có:
⦁ \(\frac{{BE}}{{EA}} = \frac{{BC}}{{AC}} = \frac{6}{5},\) suy ra \(\frac{{BE}}{{BA}} = \frac{6}{{11}}.\)
⦁ \(\frac{{AD}}{{DC}} = \frac{{AB}}{{BC}} = \frac{6}{5},\) suy ra \(\frac{{AD}}{{AC}} = \frac{2}{5}.\)
c) Gọi \({h_1},\,\,{h_2},\,\,{h_3}\) lần lượt là độ dài đường cao kẻ từ \(E\) đến \(BD;\) độ dài đường cao kẻ từ \(D\) đến \(AB;\) độ dài đường cao kẻ từ \(B\) đến \(AC.\)
Ta có: \[{S_{DIE}} = \frac{1}{2} \cdot {h_1} \cdot DI;\] \({S_{BDE}} = \frac{1}{2}{h_1} \cdot BD = \frac{1}{2}{h_2} \cdot BE;\)
\({S_{ABD}} = \frac{1}{2}{h_2} \cdot AB = \frac{1}{2}{h_3} \cdot AD;\) \({S_{ABC}} = \frac{1}{2} \cdot {h_3} \cdot AC.\)
Do đó \[\frac{{{S_{DIE}}}}{{{S_{BDE}}}} = \frac{{\frac{1}{2} \cdot {h_1} \cdot DI}}{{\frac{1}{2}{h_1} \cdot BD}} = \frac{{DI}}{{BD}} = \frac{1}{3};\] \[\frac{{{S_{BDE}}}}{{{S_{ABD}}}} = \frac{{\frac{1}{2}{h_2} \cdot BE}}{{\frac{1}{2}{h_2} \cdot AB}} = \frac{{BE}}{{AB}} = \frac{6}{{11}};\]
\[\frac{{{S_{ABD}}}}{{{S_{ABC}}}} = \frac{{\frac{1}{2}{h_3} \cdot AD}}{{\frac{1}{2}{h_3} \cdot AC}} = \frac{{AD}}{{AC}} = \frac{2}{5}.\]
Khi đó \[{S_{DIE}} = \frac{1}{3}{S_{BDE}} = \frac{1}{3} \cdot \frac{6}{{11}}{S_{ABD}} = \frac{1}{3} \cdot \frac{6}{{11}} \cdot \frac{2}{5}{S_{ABC}} = \frac{4}{{55}}{S_{ABC}}.\]
Suy ra \(\frac{{{S_{DIE}}}}{{{S_{ABC}}}} = \frac{4}{{55}}.\)
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
Cho hình vẽ bên, biết \[MN\,{\rm{//}}\,BC,\] \[NP\,{\rm{//}}\,AB\,.\]
Khẳng định nào sau đây là sai?
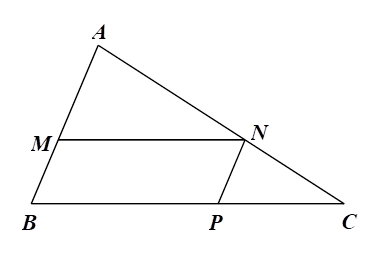
Cho hình vẽ bên, biết \[MN\,{\rm{//}}\,BC,\] \[NP\,{\rm{//}}\,AB\,.\]
Khẳng định nào sau đây là sai?

Lời giải
Hướng dẫn giải
Đáp án đúng là: D
Xét \(\Delta ABC\) với \[MN\,{\rm{//}}\,BC,\] ta có:
⦁ \(\frac{{AM}}{{AB}} = \frac{{MN}}{{BC}} = \frac{{AN}}{{AC}}\) (hệ quả của định lí Thalès). Suy ra \(\frac{{AM}}{{MN}} = \frac{{AB}}{{BC}}.\) Do đó A là khẳng định đúng.
Xét \(\Delta ABC\) với \[NP\,{\rm{//}}\,AB\,,\] ta có:
⦁ \(\frac{{AN}}{{AC}} = \frac{{BP}}{{BC}}\) (hệ quả của định lí Thalès). Do đó B là khẳng định đúng.
⦁ \(\frac{{CP}}{{BP}} = \frac{{CN}}{{AN}}\) (định lí Thalès). Do đó C là khẳng định đúng.
⦁ \(\frac{{CN}}{{AC}} = \frac{{NP}}{{AB}}\) (hệ quả của định lí Thalès).
Ta có \(AN \ne CN\) nên \(\frac{{AN}}{{AC}} \ne \frac{{CN}}{{AC}}\).
Mà \(\frac{{MN}}{{BC}} = \frac{{AN}}{{AC}}\) và \(\frac{{CN}}{{AC}} = \frac{{NP}}{{AB}}\) nên \(\frac{{MN}}{{BC}} \ne \frac{{NP}}{{AB}}.\) Do đó D là khẳng định sai.
Vậy ta chọn phương án D.
Lời giải
Hướng dẫn giải
a) 1 triệu đồng \[ = 1{\rm{ }}000\] nghìn đồng.
Hàm số biểu thị tổng chi phí \[y\] (nghìn đồng) để thuê một chiếc thuyền du lịch trong \[x\] (giờ) là: \[y = 1{\rm{ }}000 + 500x\] (nghìn đồng).
b) Đồ thị hàm số \[y = 1{\rm{ }}000 + 500x\] đi qua hai điểm \[\left( {--2;0} \right)\] và \[\left( {0;1{\rm{ }}000} \right)\] nên đồ thị hàm số được vẽ như hình dưới.
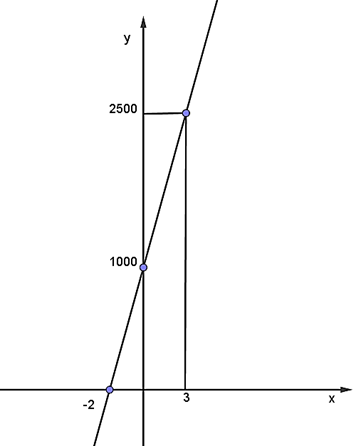
Tổng chi phí cho một lần thuê trong \[x = 3\] giờ tương ứng với điểm \[y = 2{\rm{ }}500\] nghìn đồng = 2 triệu 500 nghìn đồng.
c) Giao điểm của đồ thị với trục tung là điểm \[\left( {0;{\rm{ }}1{\rm{ }}000} \right).\] Giao điểm này biểu thị chi phí cố định khi thuê thuyền, dù không sử dụng giờ nào (tức là \[x = 0)\] vẫn phải trả phí 1 triệu đồng này, nếu đặt thuê.
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.