Dạng 2. Vận dụng kiến thức hình thoi để giải toán có đáp án

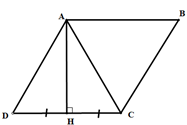
Gọi H  là chân đường cao kẻ từ A  đến cạnh CD .

Từ giả thiết ta có: $AH\perp CD,CH=HD$ .

Suy ra AH là đường trung trục của đoạn CD  nên AC = CD   (1)

Do ABCD  là hình thoi nên AD = CD (2)

Từ (1)  và (2)  suy ra AD = CD = AC  nên tam giác ACD  là tam giác đều, do đó $\widehat{D}={60}^{\circ }$ .

Ta lại có AB // CD  (Vì ABCD là hình thoi) góc A  và góc D  là hai góc trong cùng phía

Nên chúng bù nhau hay: $\widehat{A}={180}^{\circ }-\widehat{D}={180}^{\circ }-{60}^{\circ }={120}^{\circ }$

Áp dụng tính chất về góc vào hình thoi ta được: $\widehat{B}=\widehat{D}={60}^{\circ },\widehat{A}=\widehat{C}={120}^{\circ }$

Gọi hình thoi là ABCD , trung điểm của AB, BC, CD, DA  lần lượt là M, N, P, Q .

Nối đường chéo AC  và BD

Xét tam giác ABD có:

MQ là đường trung bình (qua 2 trung điểm).

Suy ra MQ // BD  và  $MQ=\frac{1}{2}BD$.     (1)

Xét tam giác CBD có NP  là đường trung bình.

Suy ra $NP//BD;NP=\frac{1}{2}BD$    (2)

Từ (1)  và (2)  suy ra MNPQ  là hình bình hành.

Ta có $AC\perp BD$  (tính chất đường chéo hình thoi)

suy ra $MN\perp MQ$  hay $\widehat{M}={90}^{\circ }$ .

Vậy tứ giác MNPQ  là hình chữ nhật (hình bình hành có 1 góc vuông).

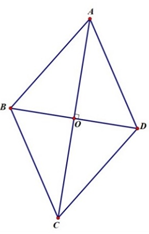
a) Hình bình hành nhận giao điểm hai đường chéo là tâm đối xứng.

Hình thoi cũng là một hình bình hành nên giao điểm hai đường chéo hình thoi là tâm đối xứng của hình.

b) BD  là đường trung trực của AC  (do BA = BC, DA = DC ) nên A  đối xứng với C qua BD .

B và D  cũng đối xứng với chính nó qua BD .

Do đó BD  là trục đối xứng với chính nó qua BD .

Vậy BD  là trục đối xứng của hình thoi.

Tương tự, AC  cũng là trục đối xứng của hình thoi.

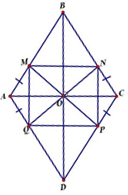
a) $\Delta AOM=\Delta COP\Rightarrow \widehat{AOM}=\widehat{COP}$  hay $\widehat{AOM};\widehat{COP}$  là hai góc đối đỉnh.

=> M, O, P thẳng hàng.