Thi Online Bài tập Toán 8 Chủ đề 13: Luyện tập đường thẳng song song với một đường thẳng cho trước có đáp án
Dạng 1. Luyện tập đường thẳng song song với một đường thẳng cho trước có đáp án
-
385 lượt thi
-
10 câu hỏi
-
45 phút
Câu 1:
Cho góc vuông xOy và điểm A thuộc tia Ox sao cho OA = 4cm. lấy điểm B tùy ý trên tia Oy và gọi M là trung điểm của AB . Khi B di chuyển trên tia Oy thì M di chuyển trên đường nào
Cho góc vuông xOy và điểm A thuộc tia Ox sao cho OA = 4cm. lấy điểm B tùy ý trên tia Oy và gọi M là trung điểm của AB . Khi B di chuyển trên tia Oy thì M di chuyển trên đường nào
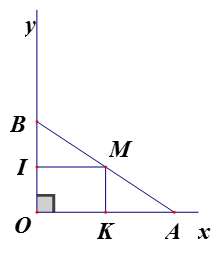
+ Kẻ
+ Tứ giác IMKO có
+ Tứ giác IMKO là hình chữ nhật
Suy ra IM = OK; MK // OI
+ Xét có M là trung điểm AB, MK // OB suy ra
+ Suy ra MI = 2cm
+ Suy ra khi B di chuyển trên tia Oy thì M di chuyển trên đường thẳng vuông góc với tia Ox tại K song song với Oy và cách Oy một khoảng 2cm
Giới hạn: Khi B trùng O thì M trùng K
khi B di chuyển trên tia Oy thì M di chuyển trên đường thẳng vuông góc với tia Ox tại K song song với Oy và cách Oy một khoảng 2cm
Vậy khi B di chuyển trên tia Oy thì M di chuyển trên tia Kt vuông góc với tia Ox tại K và cách Oy
một khoảng 2cm
Câu 2:
Cho góc vuông xOy, điểm A trên tia Oy . Điểm B di chuyển trên tia Ox . Gọi C là điểm đối xứng với A qua B . Điểm C di chuyển trên đường nào ?
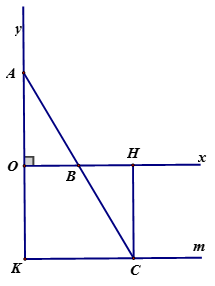
+ Vì điểm C đối xứng với AC qua B nên BA = BC
+ Kẻ
+ Xét tam giác vuông AOB và CHB có
+ Có ( đối đỉnh)
+ Do đó nên CH = AO
MÀ OA không đổi nên CH không đổi
+ Suy ra C chuyển động trên đường thẳng song song với Ox cách Ox một khoảng bằng
Khi B trùng O thì C trùng K đối xứng với A qua O
Vậy C chuyển động trên tia Km // Ox cách Ox một khoảng không đổi bằng oa
Câu 3:
Cho điểm A nằm ngoài đường thẳng d . Điểm M di chuyển trên đường thẳng d . Gọi B là điểm đối xứng với A qua M. Điểm B di chuyển trên đường nào?
Cho điểm A nằm ngoài đường thẳng d . Điểm M di chuyển trên đường thẳng d . Gọi B là điểm đối xứng với A qua M. Điểm B di chuyển trên đường nào?
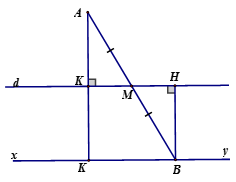
+ Kẻ
+ Có AM = MB
+ Chứng minh
+ Suy ra AK = BH
+ Điểm A cố định, đường thẳng d cố định nên AK không thay đổi
Vậy B chuyển động trên đường thẳng xy song song với d cách d một khoảng bằng AKCâu 4:
Cho hình bình hành ABCD có cạnh AB = 2cm. Gọi I là giao điểm của AC và BD. Điểm I chuyển động trên đường nào?
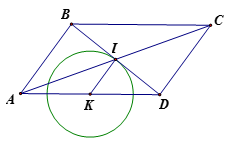
+ Gọi K là trung điểm AD. Ta có AD cố định nên K cố định
+ Trong ta có
IB = ID ( tính chất hình bình hành)
KA = KD ( theo cách vẽ)
Nên KI là đường trung bình của
Suy ra KI = AB : 2 = 2 : 2 = 1 (tính chất đường trung bình)
+ B , C thay đổi thì I thay đổi luôn cách K cố định một khoảng không đổi nên I chuyển động trên đường tròn (K,1cm)
Vậy B chuyển động trên đường thẳng xy song song với d cách d một khoảng bằng AKCâu 5:
Cho tam giác ABC cân tại A, các điểm M, N theo thứ tự di động trên các cạnh AB, AC sao cho AM = CN. Hãy tìm tập hợp trung điểm I của MN
Cho tam giác ABC cân tại A, các điểm M, N theo thứ tự di động trên các cạnh AB, AC sao cho AM = CN. Hãy tìm tập hợp trung điểm I của MN
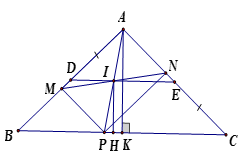
+ Kẻ NP // AB ta có ( 2 góc đồng vị); mà (GT)
Suy ra hay NPC cân
Suy ra NP = NC mà NC = MA nên NP = MA
Mà NP // MA nên tứ giác AMPN là hình bình hành có I là trung điểm MN
Suy ra I là trung điểm AP
+ Kẻ IH và AK cùng vuông góc với BC ta có IH là đường trung bình của APK nên (không đổi)
Vậy tập hợp các trung điểm I của MN khi M, N di động trên AB, AC là đường trung bình của ABC và DE // BC trong đó D là trung điểm cạnh AB, E là trung điểm cạnh ACCác bài thi hot trong chương:
( 1 K lượt thi )
( 894 lượt thi )
( 1 K lượt thi )
( 584 lượt thi )
( 2 K lượt thi )
( 1.8 K lượt thi )
( 1.7 K lượt thi )
( 1.7 K lượt thi )
( 1.3 K lượt thi )
Đánh giá trung bình
0%
0%
0%
0%
0%