Cho tam giác nhọn ABC, các đường cao BD, CE. Gọi H, K thứ tự là chân các đường vuông góc kẻ từ B và C đến đường thẳng DE. Chứng minh rằng HE = DK
Quảng cáo
Trả lời:
Giải bởi Vietjack
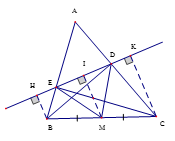
Vì BD, CE là các đường cao của ABC nên , do đó BDC vuông tại D, CEB vuông tại E.
Gọi M là trung điểm của BC, vẽ DM, EM thì DM, EM là các trung tuyến ứng với cạnh huyền của BDC và CEB.
Áp dụng tính chất đường trung tuyến ứng với cạnh huyền vào 2 tam giác vuông trên, ta được:
cân tại M
Từ giả thiết ta có tứ giác BKHC là hình thang vuông nên vẽ thêm thì BH // MI // CK (1)
Mà BM = MC (cách vẽ) (2)
Từ (1) và (2) suy ra BH, MI, CK là ba đường thẳng song song cách đều nên chúng chắn trên đường thẳng HK hai đoạn thẳng liên tiếp bằng nhau là HI = IK (3)
Ta có DM = EM suy ra MDE cân tại M , có MI là đường cao ứng vói cạnh đáy DE nên EI = ID (4)
Trừ theo vế đẳng thức (3) cho (4) ta được EH = DKĐăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
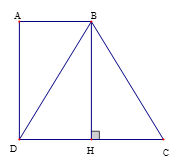
Vẽ hình xong ta dự đoán rằng BDC đều. Để chứng minh BDC đều ta chỉ cần chứng minh BDC cân đỉnh B là đủ.
Suy ra ta cần vẽ thêm đường phụ ,
Vẽ
Ta có nên AD // DH.
Mặt khác AB // DC, AD // BH nên AB = DH ( tính chất đoạn chắn)
Mà DC = 2AB (GT) và AB = DH => DC = 2DH
Suy ra H là trung điểm của DC.
BDC có BH là đường cao và là trung tuyến nên BDC cân tại B
Suy ra đều
Mà (vì AB // DC ) do đó :
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
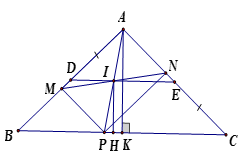
+ Kẻ NP // AB ta có ( 2 góc đồng vị); mà (GT)
Suy ra hay NPC cân
Suy ra NP = NC mà NC = MA nên NP = MA
Mà NP // MA nên tứ giác AMPN là hình bình hành có I là trung điểm MN
Suy ra I là trung điểm AP
+ Kẻ IH và AK cùng vuông góc với BC ta có IH là đường trung bình của APK nên (không đổi)
Vậy tập hợp các trung điểm I của MN khi M, N di động trên AB, AC là đường trung bình của ABC và DE // BC trong đó D là trung điểm cạnh AB, E là trung điểm cạnh ACĐăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập