Câu hỏi:
12/07/2024 1,181
Cho tứ giác ABCD có AD = BC. Gọi E, F, M, N lần lượt là trung điểm của AB, DC, DB, AC. Chứng minh tứ giác EFMN là hình thoi.
Cho tứ giác ABCD có AD = BC. Gọi E, F, M, N lần lượt là trung điểm của AB, DC, DB, AC. Chứng minh tứ giác EFMN là hình thoi.
Câu hỏi trong đề: Bài tập Toán 8 Chủ đề 16: Luyện tập hình thoi có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
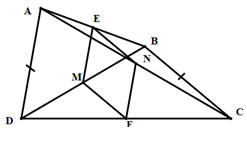
Vì E, M lần lượt là trung điểm của AB, BD nên:
EM là đường trung bình của .
Do đó:
Vì N, F lần lượt là trung điểm của AC, DC nên:
NF là đường trung bình của ACD . Do đó:
Từ (1), (2) suy ra EMFN là hình bình hành. (*)
Vì E, N lần lượt là trung điểm của AB, AC nên:
EN là đường trung bình của ABC . Do đó:
Mà AD = BC (giả thiết) (4)
Từ (1), (3), (4) ta được: EM = EN (**)
Từ (*) và (**) ta được tứ giác EMFNlà hình thoi. (đpcm).
Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
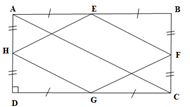
Vì E, F lần lượt là trung điểm của AB, BC nên:
EFlà đường trung bình của . Do đó:
Vì G, H lần lượt là trung điểm của CD, DA nên:
GH là đường trung bình của . Do đó:
Từ (1) và (2) suy ra:
Vậy tứ giác EFGH là hình bình hành
Xét và có:
EA = EB (Giả thiết)
AH = BF (Vì AD = BC)
Suy ra:
=> HE = FE (**)
Từ (*) và (**) ta được tứ giác là hình thoi (đpcm).
Lời giải
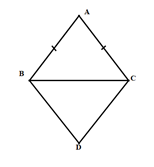
Xét tứ giác ABDC có:
AB // CD; AC // BD (gt)
=> tứ giác ABDC là hình bình hành.
Lại có: AB = AC ( cân tại A )
Nên tứ giác ABDC là hình thoi. (đpcm)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo