Trong phép chia có dư aa chia cho b, trong đó b ≠ 0, ta luôn tìm được đúng hai số tự nhiên q và r duy nhất sao cho:
a = b.q + r
Khẳng định nào sau đây đúng?
A. r ≥ b
B. 0 < b < r
C. 0 < r < b
D. 0 ≤ r < b
Quảng cáo
Trả lời:
Giải bởi Vietjack
Khi chia a cho b, trong đó b ≠ 0, ta luôn tìm được đúng hai số tự nhiên q và r duy nhất sao cho:
a = b.q + r trong đó 0 ≤ r < b
Phép chia a cho b là phép chia có dư nên r ≠ 0
Vậy 0 < r < b.
Đáp án cần chọn là: C
Hot: 1000+ Đề thi giữa kì 1 file word cấu trúc mới 2025 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
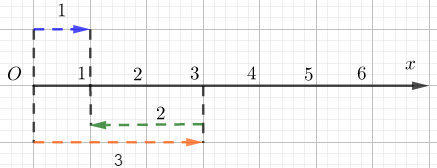
Câu 1
A. Phép cộng của 1 và 2
B. Phép trừ của 3 và 2
C. Phép cộng của 1 và 3
D. Phép trừ của 3 và 1
Lời giải
Số 3 và số 1 cùng chiều từ trái sang phải, số 2 ngược chiều với hai số này.
Mà ta có 3 – 2 = 1 nên hình ảnh trên minh họa cho phép trừ 3 - 2.
Đáp án cần chọn là: B
Câu 2
A. 3k(k ∈ N)
B. 5k + 3(k∈N)
C. 3k + 1(k∈N)
D. 3k + 2(k∈N)
Lời giải
Các số hạng chia hết cho 33 có dạng tổng quát là x = 3k(k∈N)
Đáp án cần chọn là: A
Câu 3
A. 1
B. 2
C. 3
D. 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. 445 = 13.34 + 3
B. 445 = 13.3 + 34
C. 445 = 34.3 + 13
D. 445 = 13.34
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo