Câu hỏi:
17/05/2022 2,867
Trong thí nghiệm giao thoa trên mặt nước, hai nguồn sóng kết hợp S1 và S2 dao động cùng pha, cùng tần số, cách nhau \[{S_1}{S_2} = 7cm\] tạo ra hai sóng kết hợp có bước song λ = 2cm. Một đường thẳng (Δ) song song với \[{S_1}{S_2}\] và cách \[{S_1}{S_2}\] một khoảng là 2 cm và cắt đường trung trực của \[{S_1}{S_2}\]tại điểm C. Khoảng cách lớn nhất từ C đến điểm dao động với biên độ cực đại trên (Δ) là
Đáp án chính xác
Câu hỏi trong đề: 30 đề thi thử THPT Quốc gia môn Vật lí năm 2022 có lời giải !!
Bắt đầu thiQuảng cáo
Trả lời:
Giải bởi Vietjack
Phương pháp:
+ Sử dụng biểu thức tính số điểm dao động cực đại trên đường thẳng nối 2 nguồn cùng pha: \[ - \frac{{{S_1}{S_2}}}{\lambda } < k < \frac{{{S_1}{S_2}}}{\lambda }\]
+ Vận dụng biểu thức xác định vị trí cực đại giao thoa: \[{d_2} - {d_1} = k\lambda \]
+ Sử dụng hệ thức trong tam giác.
Cách giải:
Ta có:
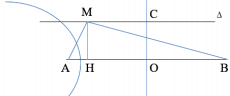
Gọi M là cực đại trên Δ xa C nhất.
Số cực đại trên AB bằng số giá trị k nguyên thỏa mãn:
⇒ M là cực đại bậc 3
Ta có: \[MB - MA = 3\lambda \]
Gọi H – là hình chiếu của M trên AB
+ Trường hợp H nằm trong AB:
+ Trường hợp H nằm ngoài AB:
Chọn D.
Nhà sách vietjack
Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Hai nguồn điện giống nhau ghép song song, mỗi nguồn có suất điện động ξ. Suất điện động của bộ nguồn là
Xem đáp án »
17/05/2022
9,907
Câu 2:
Điện năng truyền tải từ nơi phát đến nơi tiêu thụ bằng đường dây một pha. Coi công suất truyền đi là không đổi và hệ số công suất luôn bằng 1. Nếu tăng điện áp truyền tải từ U lên \[(U + 100)(kV)\]thì công suất hao phí trên đường dây giảm 4 lần. Nếu tăng điện áp truyền tải từ U lên \[(U + 300)(kV)\]thì công suất hao phí trên đường dây giảm
Xem đáp án »
17/05/2022
3,513
Câu 3:
Trong thí nghiệm Y-âng về giao thoa ánh sáng, gọi λ là bước sóng ánh sáng đơn sắc dùng trong thí nghiệm, a là khoảng cách giữa hai khe Y-âng, D là khoảng cách từ mặt phẳng chứa hai khe đến màn quan sát. Khoảng cách giữa hai vân tối liền kề là
Xem đáp án »
17/05/2022
1,834
Câu 4:
Một con lắc lò xo treo thẳng đứng gồm lò xo nhẹ có độ cứng 100 N/m và vật nhỏ có khối lượng m = 625g dao động điều hòa với biên độ 5 cm tại nơi có gia tốc trọng trường \[g = 10m{\rm{/}}{s^2}.\] Lấy \[{\pi ^2} \approx 10\]và bỏ qua sức cản của không khí. Tại thời điểm vật nhỏ con lắc qua vị trí cân bằng hướng lên, một vật nhỏ có khối lượng m' = 50g được bắn thẳng đứng lên từ một vị trí nằm trên trục lò xo và cách vị trí cân bằng của con lắc 56,25 cm với tốc độ 3,5 m/s . Sau đó, hai vật nhỏ va chạm và dính vào nhau cùng dao động. Biên độ dao động của con lắc sau va chạm gần đúng với giá trị nào sau đây?
Xem đáp án »
17/05/2022
1,407
🔥 Đề thi HOT:
-
(2025 mới) Đề ôn thi tốt nghiệp THPT Vật lí (Đề số 1)
-
Đề minh họa tốt nghiệp THPT môn Vật lý có đáp án năm 2025 (Đề 2)
-
(2025 mới) Đề ôn thi tốt nghiệp THPT Vật lí (Đề số 2)
-
Đề minh họa tốt nghiệp THPT môn Vật lý có đáp án năm 2025 (Đề 4)
-
Đề minh họa tốt nghiệp THPT môn Vật lý có đáp án năm 2025 (Đề 3)
-
(2025 mới) Đề ôn thi tốt nghiệp THPT Vật lí (Đề số 6)
-
Đề thi thử tốt nghiệp THPT môn Vật lí Cụm các trường THPT , Các trung tâm GDTX , GDNN - GDTX Tỉnh Bắc Ninh có đáp án
-
Đề thi thử tốt nghiệp THPT môn Vật lí THPT Chuyên Phan Bội Châu- Nghệ An - lần 1 có đáp án
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận