Câu hỏi:

20/06/2022 1,032

Cho hình vẽ

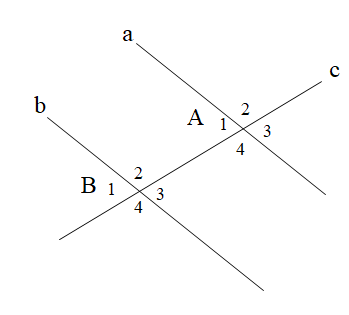
Biết một cặp góc đồng vị \[\widehat {{A_4}} = \widehat {{B_4}} = 60^\circ \]. Tính số đo của cặp góc đồng vị \[\widehat {{A_3}}\] và \[\widehat {{B_3}}\].

A. 120°;

Đáp án chính xác

B. 50°;

C. 60°;

D. 150°.

Câu hỏi trong đề: 15 câu Trắc nghiệm Toán 7 KNTT Bài 9: Hai đường thẳng song song và dấu hiệu nhận biết có đáp án !!

Trả lời:

Giải bởi Vietjack

Đáp án đúng là: A

Ta có:

\[\widehat {{A_4}} + \widehat {{B_3}} = 180^\circ \] (hai góc kề bù)

Do đó \[\widehat {{B_3}} = 180^\circ - 60^\circ = 120^\circ \]

Suy ra \[\widehat {{A_3}}\; = \widehat {{B_3}} = 120^\circ \]

Vậy chọn đáp án A.

Bình luận hoặc Báo cáo
về câu hỏi!

Câu 1:

Cho \(\widehat {xOy} = 66^\circ \), tia Ot là tia phân giác của góc xOy. Số đo góc xOt là:

A. 33°;

B. 44°;

C. 66°;

D. 111°.

Xem đáp án » 20/06/2022 1,354

Câu 2:

Cho hình vẽ

Biết x // y, \[\widehat {{H_3}} = 39^\circ .\]Tính \[\widehat {{H_3}} + \widehat {{K_4}}\].

A. 180°;

B. 141°;

C. 120°;

D. 138°.

Xem đáp án » 20/06/2022 1,194

Câu 3:

Cho tia Ot nằm trong góc mOn, \[\widehat {mOt} = \widehat {tOn}\] thì

A. Ot là tia phân giác của góc mOn;

B. Ot là tia nằm phía trong của góc mOn;

C. Ot là tia nằm phía ngoài của góc mOn;

D. Ot là tia nằm giữa hai cạnh Om và On.

Xem đáp án » 20/06/2022 1,178

Câu 4:

Cho \[\widehat {MON} = 90^\circ \] và vẽ tia OP sao cho tia ON là tia phân giác của góc MOP. Khi đó góc MOP là:

A. Góc tù;

B. Góc bẹt;

C. Góc vuông;

D. Góc nhọn.

Xem đáp án » 20/06/2022 1,118

Câu 5:

Tính số đo của góc aOb. Biết \[\widehat {zOb} = 48^\circ \], Oz là tia phân giác của góc aOb.

A. 80°;

B. 96°;

C. 120°;

D. 130°.

Xem đáp án » 20/06/2022 1,001

Câu 6:

Cho hình vẽ bên dưới. Tính \(\widehat {BEF}\), biết FE // BC và \(\widehat {EBC} = 30^\circ \).

A. 60^o;

B. 120^o;

C. 30^o;

D.140^o.

Xem đáp án » 20/06/2022 949

Xem thêm các câu hỏi khác »

Cho hình vẽ

Biết một cặp góc đồng vị \[\widehat {{A_4}} = \widehat {{B_4}} = 60^\circ \]. Tính số đo của cặp góc đồng vị \[\widehat {{A_3}}\] và \[\widehat {{B_3}}\].

Nhà sách VIETJACK:

Cho \(\widehat {xOy} = 66^\circ \), tia Ot là tia phân giác của góc xOy. Số đo góc xOt là:

Cho hình vẽ

Biết x // y, \[\widehat {{H_3}} = 39^\circ .\]Tính \[\widehat {{H_3}} + \widehat {{K_4}}\].

Cho tia Ot nằm trong góc mOn, \[\widehat {mOt} = \widehat {tOn}\] thì

Cho \[\widehat {MON} = 90^\circ \] và vẽ tia OP sao cho tia ON là tia phân giác của góc MOP. Khi đó góc MOP là:

Tính số đo của góc aOb. Biết \[\widehat {zOb} = 48^\circ \], Oz là tia phân giác của góc aOb.

Cho hình vẽ bên dưới. Tính \(\widehat {BEF}\), biết FE // BC và \(\widehat {EBC} = 30^\circ \).

Bình luận

🔥 Đề thi HOT:

VIP +3 tháng ( 199,000 VNĐ )

VIP +6 tháng ( 299,000 VNĐ )

VIP +12 tháng ( 499,000 VNĐ )

Cho hình vẽ Biết một cặp góc đồng vị \[\widehat {{A_4}} = \widehat {{B_4}} = 60^\circ \]. Tính số đo của cặp góc đồng vị \[\widehat {{A_3}}\] và \[\widehat {{B_3}}\].

Nhà sách VIETJACK:

Cho \(\widehat {xOy} = 66^\circ \), tia Ot là tia phân giác của góc xOy. Số đo góc xOt là:

Cho hình vẽ Biết x // y, \[\widehat {{H_3}} = 39^\circ .\]Tính \[\widehat {{H_3}} + \widehat {{K_4}}\].

Cho tia Ot nằm trong góc mOn, \[\widehat {mOt} = \widehat {tOn}\] thì

Cho \[\widehat {MON} = 90^\circ \] và vẽ tia OP sao cho tia ON là tia phân giác của góc MOP. Khi đó góc MOP là:

Tính số đo của góc aOb. Biết \[\widehat {zOb} = 48^\circ \], Oz là tia phân giác của góc aOb.

Cho hình vẽ bên dưới. Tính \(\widehat {BEF}\), biết FE // BC và \(\widehat {EBC} = 30^\circ \).

Bình luận

🔥 Đề thi HOT:

VIP +3 tháng ( 199,000 VNĐ )

VIP +6 tháng ( 299,000 VNĐ )

VIP +12 tháng ( 499,000 VNĐ )

CHỌN BỘ SÁCH BẠN MUỐN XEM

Đăng ký

Đăng nhập

Quên mật khẩu

Cho hình vẽ

Biết một cặp góc đồng vị \[\widehat {{A_4}} = \widehat {{B_4}} = 60^\circ \]. Tính số đo của cặp góc đồng vị \[\widehat {{A_3}}\] và \[\widehat {{B_3}}\].

Cho hình vẽ

Biết x // y, \[\widehat {{H_3}} = 39^\circ .\]Tính \[\widehat {{H_3}} + \widehat {{K_4}}\].