Quảng cáo
Trả lời:
Giải bởi Vietjack
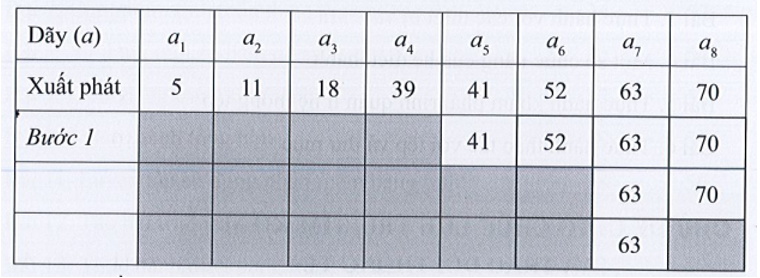
2) Số phải tìm là x = 60:
Chia đôi lần 1: Phạm vi tìm kiếm là dãy a1 đến a8. Lấy a4 là số có vị trí giữa dãy.
Vì x > a4 nên có nửa đầu dãy (có nền màu xám nhạt) chắc chắn không chứa x = 60, tiếp theo chỉ cần tìm trong nửa sau của dãy. Như vậy, phạm vi cần tìm tiếp theo là dãy con từ a5 đến a8.
Chia đôi lần 2: lấy a6 là số có vị trí giữa dãy còn lại.
Vì x > a6 nên nửa đầu dãy (có nền màu xám nhạt) chắc chắn không chứa x = 60, tiếp theo chỉ cần tìm trong nửa sau của dãy. Như vậy, phạm vi tìm kiếm tiếp theo là dãy con từ a7 đến a8.
Chia đôi lần 3: lấy a7 là số có vị trí giữa dãy còn lại.
Vì x < a7 nên nửa sau dãy (có nền màu xám nhạt) chắc chắn không chứa x = 60, tiếp theo chỉ cần tìm trong nửa dãy. Như vậy, phạm vi tìm kiếm tiếp theo là dãy con một phần tử là a7.
Chỉ còn một phần tử, không chia đôi nữa, so sánh thấy x khác a7. Kết luận: Không tìm thấy.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Dãy xuất phát:
1) Số phải tìm là x (x = 39). Các bước thực hiện tìm kiếm:
2) Số phải tìm là x (x = 60). Các bước thực hiện tìm kiếm:
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
1) Số phải tìm là x = 39:
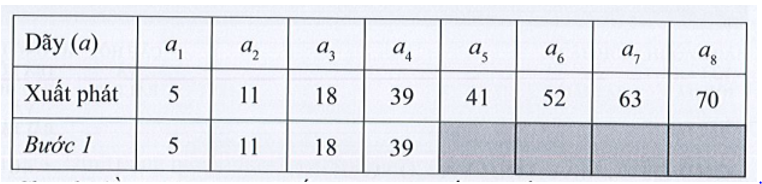
Chia đôi lần 1: Phạm vi tìm kiếm là dãy a1 đến a8. Lấy a4 là số có vị trí giữa dãy. Vì x = a4 nên đã tìm thấy x = 39 tại vị trí thứ tư.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập