Câu hỏi:
01/08/2022 5,619
Một ô tô đang đi trên đường thẳng với tốc độ không đổi 24 m/s. Ô tô này đã chạy quá tốc độ và vượt qua một cảnh sát giao thông đang ngồi trên một xe mô tô đứng yên. Người cảnh sát ngay lập tức đuổi theo ô tô với gia tốc 2,1 m/s2. Kể từ thời điểm ô tô vượt qua xe cảnh sát:
Sau bao lâu thì xe cảnh sát đuổi kịp ô tô?
Một ô tô đang đi trên đường thẳng với tốc độ không đổi 24 m/s. Ô tô này đã chạy quá tốc độ và vượt qua một cảnh sát giao thông đang ngồi trên một xe mô tô đứng yên. Người cảnh sát ngay lập tức đuổi theo ô tô với gia tốc 2,1 m/s2. Kể từ thời điểm ô tô vượt qua xe cảnh sát:
Sau bao lâu thì xe cảnh sát đuổi kịp ô tô?
Câu hỏi trong đề: Giải SBT Lí 10 Bài 5: Chuyển động biến đổi có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Lời giải
Chọn chiều dương là chiều chuyển động của ô tô. Ô tô và người cảnh sát trong trường hợp này chuyển động cùng chiều dương.
Gọi thời gian từ thời điểm ô tô bắt đầu vượt đến thời điểm cảnh sát đuổi kịp ô tô là t.
Quãng đường ô tô đi được từ thời điểm bắt đầu vượt qua cảnh sát đến thời điểm gặp nhau được xác định là: \[{s_1} = 24t\]
Quãng đường cảnh sát đuổi đến khi gặp ô tô là:
\[{s_2} = \frac{1}{2}a{t^2} = \frac{1}{2}.2,1.{t^2} = 1,05{t^2}\]
Khi gặp nhau, quãng đường xe ô tô và cảnh sát đi được bằng nhau:
\[{s_1} = {s_2} \Leftrightarrow 24t = 1,05{t^2} \Leftrightarrow t = 22,9\,s\] (vì \(t \ne 0\))
Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay
Sách thầy cô Vietjack biên soạn:
- Sách - Sổ tay kiến thức trọng tâm Vật lí 10 VietJack - Sách 2025 theo chương trình mới cho 2k9 ( 31.000₫ )
- Trọng tâm Lí, Hóa, Sinh 10 cho cả 3 bộ KNTT, CTST và CD VietJack - Sách 2025 ( 40.000₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Lời giải
Thời gian để vận động viên đạt tốc độ tối đa 9 m/s là:
\[t = \frac{{v - {v_0}}}{a} = \frac{{9 - 0}}{6} = 1,5\,s\]
Lời giải
Lời giải
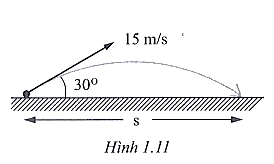
Thành phần theo phương ngang của vận tốc quả bóng là:
\[{v_x} = {v_0}\cos 30^\circ = \frac{{{v_0}\sqrt 3 }}{2}\]
Thành phần theo phương thẳng đứng của vận tốc quả bóng là:
\[{v_y} = {v_0}\sin 30^\circ = \frac{{{v_0}}}{2}\]
Quả bóng chạm đất khi:
\[h = {v_0}\sin 30^\circ t - \frac{1}{2}g{t^2} = 0 \Rightarrow t = \frac{{2{v_0}\sin {{30}^0}}}{g}\]
Tầm bay xa của quả bóng:
\[L = s = {v_0}\cos 30^\circ t = \frac{{2v_0^2sin30^\circ \cos 30^\circ }}{g} = \frac{{v_0^2.\sin {{60}^0}}}{g}\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
BÀI TOÁN ĐẠN NỔ CÓ LỜI GIẢI CHI TIẾT
-
Bộ 3 đề thi học kì 2 Vật lí 10 Kết nối tri thức cấu trúc mới có đáp án (Đề 1)
-
Đề kiểm tra giữa học kì 2 Vật lí 10 Chân trời sáng tạo có đáp án (Đề 1)
-
12 Bài tập mômen lực có đáp án
-
Đề kiểm tra giữa học kì 2 Vật lí 10 Kết nối tri thức có đáp án (Đề 1)
-
28 câu trắc nghiệm Chuyển động tròn đều cực hay có đáp án
-
Đề kiểm tra giữa học kì 2 Vật lí 10 Cánh diều có đáp án (Đề 2)
-
40 câu trắc nghiệm lí thuyết chuyển động, chuyên động thẳng đều có đáp án
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận