Quảng cáo
Trả lời:
Lời giải
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Lời giải
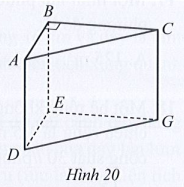
Diện tích đáy ABC của hình lăng trụ là:
25 : 5 = 5 (cm2).
Công thức tính diện tích đáy là tam giác ABC vuông tại B là:
SABC = \(\frac{1}{2}.\)AB.BC
Do đó độ dài cạnh BC là:
BC = \(\frac{{2{S_{ABC}}}}{{AB}} = \frac{{2.5}}{2}\) = 5 (cm).
Vậy độ dài cạnh BC là 5 cm.
Lời giải
Lời giải
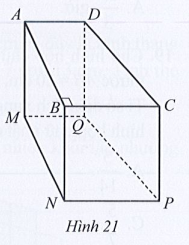
• Diện tích đáy tam giác ABC vuông tại B là:
SABC = \(\frac{1}{2}\)AB.BC = \(\frac{1}{2}\).20.15 = 150 (cm2).
Thể tích của hình lăng trụ đứng tam giác ABC.MNP là:
SABC.BN (cm3).
• Diện tích đáy hình thang ABCD vuông tại B là:
SABCD = \(\frac{1}{2}\)(AD + BC).AB = \(\frac{1}{2}\).(11 + 15).20 = 260 (cm2).
Thể tích của hình lăng trụ đứng tứ giác ABCD.MNPQ là:
SABCD.BN (cm3).
Tỉ số giữa thể tích của hình lăng trụ đứng tam giác ABC.MNP và thể tích của hình lăng trụ đứng tứ giác ABCD.MNPQ là:
\(\frac{{{V_{ABC.MNP}}}}{{{V_{ABCD.MNPQ}}}} = \frac{{{S_{ABC}}.BN}}{{{S_{ABCD}}.BN}} = \frac{{{S_{ABC}}}}{{{S_{ABCD}}}} = \frac{{150}}{{260}} = \frac{{15}}{{26}}.\)
Vậy tỉ số cần tìm bằng \(\frac{{15}}{{26}}.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.