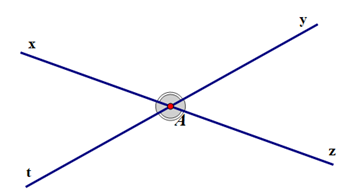
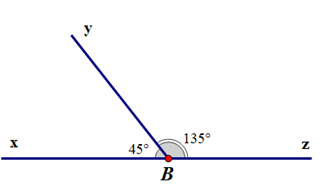
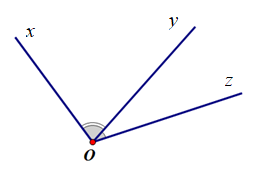
Cho hình vẽ sau, khẳng định nào sau đây sai?

Quảng cáo
Trả lời:
Hướng dẫn giải:
Đáp án đúng là: D
+ Ta có: \(\widehat {xBy},\widehat {yBz}\)là hai góc có một cạnh chung Oy và hai cạnh Bx, Bz nằm trên hai nửa mặt phẳng đối nhau bờ chứa cạnh chung By.
Suy ra \(\widehat {xBy},\widehat {yBz}\) là hai góc kề nhau.
Suy ra khẳng định A đúng.
+ Có \(\widehat {xBy} = {45^o},\widehat {yBz} = {135^o}\)
Suy ra \(\widehat {xBy} + \widehat {yBz} = {45^o} + {135^o} = {180^o}\)
Khi đó \(\widehat {xBy},\widehat {yBz}\) là hai góc bù nhau.
Suy ra khẳng định B đúng.
+ Vì \(\widehat {xBy},\widehat {yBz}\) là hai góc vừa kề nhau vừa bù nhau nên \(\widehat {xBy},\widehat {yBz}\) là hai góc kề bù.
Suy ra khẳng định C đúng.
+ Hai góc \(\widehat {xBy}\) và \(\widehat {yBz}\) có tia Bx là tia đối của tia Bz. Tuy nhiên tia By của \(\widehat {xBy}\)không là tia đối với tia nào của \(\widehat {yBz}\).
Suy ra \(\widehat {xBy}\) và \(\widehat {yBz}\) không là hai góc đối đỉnh.
Vậy khẳng định D sai.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
Lời giải
Hướng dẫn giải:
Đáp án đúng là: D
+ Hai đường thẳng cắt nhau tạo thành hai cặp góc đối đỉnh.
Ví dụ hai đường thẳng xx’ và yy’ cắt nhau tại A sẽ tạo thành hai cặp góc đối đỉnh là \(\widehat {xAy}\) và \(\widehat {x'Ay'}\); \(\widehat {xAy'}\) và \(\widehat {x'Ay}\).
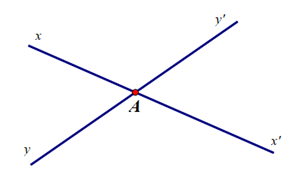
Do đó khẳng định D đúng.
+ Khẳng định A, B, C sai vì:
Hai góc có tổng bằng 180° là hai góc bù nhau.
Hai góc vừa kề nhau, vừa bù nhau là hai góc kề bù.
Hai góc kề nhau là hai góc có một cạnh chung và hai cạnh còn lại nằm khác phía đối với đường thẳng chứa cạnh chung đó.
Câu 2
Lời giải
Hướng dẫn giải:
Đáp án đúng là: B
Hai góc đối đỉnh thì bằng nhau nhưng hai góc bằng nhau thì chưa chắc đã đối đỉnh. Dưới đây là một số ví dụ về trường hợp hai góc bằng nhau nhưng không đối đỉnh:
Hai góc kề bù là hai góc vừa kề nhau, vừa bù nhau.
Do đó các khẳng định (I), (III) đúng. Khẳng định (II) sai.
Vậy có 2 khẳng định đúng.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
 ;
;B.
 ;
;
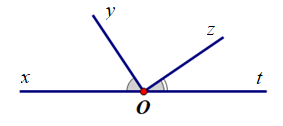 ;
;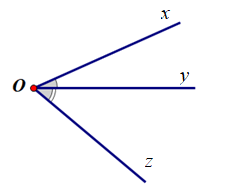 .
.Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.