Câu hỏi:

09/08/2022 468

Tia Am là phân giác của \(\widehat {bAc}\) nếu:

A. Am nằm giữa hai tia Ab và Ac;

B. \(\widehat {bAm} = \widehat {mAc}\);

C. Ab nằm giữa hai tia Am và Ac; \(\widehat {bAm} = \widehat {mAc}\);

D. \(\widehat {bAc} = \widehat {bAm} + \widehat {mAc}\) và \(\widehat {bAm} = \widehat {mAc}\).

Xem lời giải

Câu hỏi trong đề: 14 Bài tập Nhận biết và vẽ tia phân giác của một góc (có lời giải) !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

Hướng dẫn giải:

Đáp án đúng là: D

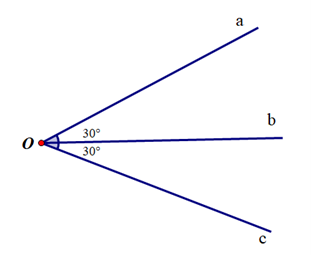
Ta có \(\widehat {bAc} = \widehat {bAm} + \widehat {mAc}\) suy ra Am nằm giữa hai tia Ab và Ac.

Mà \(\widehat {bAm} = \widehat {mAc}\).

Do đó Am là tia phân giác \(\widehat {bAc}\).

Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

Bình luận

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Cho tia Ob nằm giữa hai tia Oa và Oc; \(\widehat {aOb} = \widehat {bOc} = {20^o}\). Khẳng định nào sau đây sai?

A. \(\widehat {AOC} = {40^o}\);

B. Ob là tia phân giác \(\widehat {aOc}\);

C. \(\widehat {aOb}\) và \(\widehat {bOc}\) là hai góc kề nhau;

D. Oc là tia phân giác \(\widehat {aOb}\).

Lời giải

Hướng dẫn giải:

Đáp án đúng là: D

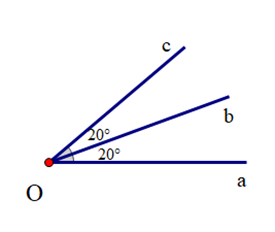
Media VietJack

+ Do Ob nằm giữa hai tia Oa và Oc nên:

\(\widehat {aOc} = \widehat {aOb} + \widehat {bOc}\) = 20° + 20° = 40°.

Do đó khẳng định A đúng.

+ Ta có Ob nằm giữa hai tia Oa và Oc và \(\widehat {aOb}\) = \(\widehat {bOc}\) = 20°

Suy ra Ob là tia phân giác \(\widehat {aOc}\).

Do đó khẳng định B đúng.

+ \(\widehat {aOb}\) và \(\widehat {bOc}\) là hai góc có chung cạnh Ob; hai tia Oa, Oc nằm khác phía với đường thẳng chứa cạnh Ob.

Suy ra \(\widehat {aOb}\) và \(\widehat {bOc}\) là hai góc kề nhau.

Do đó khẳng định C đúng.

+ Do Oc không nằm giữa hai tia Oa và Ob nên Oc không là tia phân giác của \(\widehat {aOb}\).

Do đó khẳng định D sai.

Câu 2

Tia Ob là phân giác của \(\widehat {aOc}\) trong hình vẽ nào dưới đây?

;

Lời giải

Hướng dẫn giải:

Đáp án đúng là: B

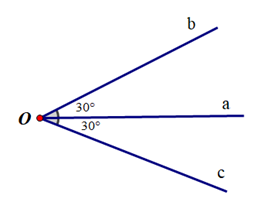
Đáp án A: Tia Ob không nằm giữa hai tia Oa và Oc nên Ob không là tia phân giác của \(\widehat {aOc}\).

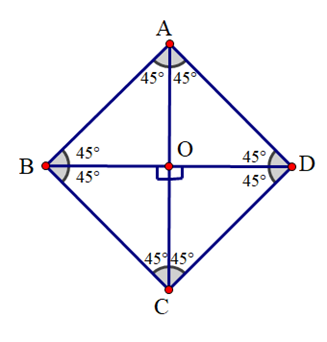
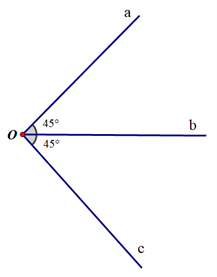
Đáp án B: Tia Ob nằm giữa hai tia Oa và Oc; \(\widehat {aOb} = \widehat {bOc}\) (cùng bằng 45°). Do đó Ob là tia phân giác của \(\widehat {aOc}\).

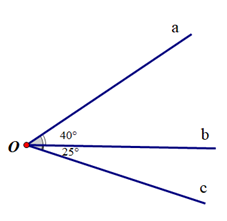
Đáp án C: Tia Ob nằm giữa hai tia Oa và Oc; \(\widehat {aOb} \ne \widehat {bOc}\) (do 40° ≠ 25°) nên Ob không là tia phân giác của \(\widehat {aOc}\).

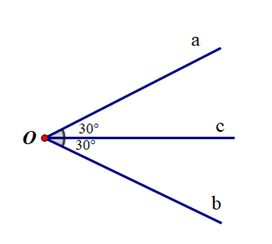
Đáp án D: Tia Ob không nằm giữa hai tia Oa và Oc nên Ob không là tia phân giác của \(\widehat {aOc}\).

Như vậy tia Ob là phân giác của \(\widehat {aOc}\) trong hình vẽ ở đáp án B.

Câu 3

Cho hình vẽ sau và cho biết tia OC là tia phân giác của góc nào?

A. \(\widehat {BAD}\);

B. \(\widehat {BOD}\);

C. \(\widehat {BCD}\);

D. \(\widehat {ABC}\).

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 4

Cho hình vẽ sau:

Tia Oy là tia phân giác của góc nào?

A. \(\widehat {xOz}\);

B. \(\widehat {yOt}\);

C. \(\widehat {xOt}\);

D. \(\widehat {yOz}\).

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 5

Quan sát hình vẽ sau và cho biết tia Ob có là tia phân giác của \(\widehat {aOc}\) không? Vì sao?

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 6

Xét bài toán: "Cho \(\widehat {xOy} = {70^o}\). Nêu cách dựng tia phân giác của \(\widehat {xOy}\) bằng compa". Hãy sắp xếp một cách hợp lý các câu sau đây để có lời giải của bài toán trên.

(I). Dựng hai cung tròn tâm A và B có cùng bán kính sao cho chúng cắt nhau tại một điểm M nằm trong góc \(\widehat {xOy}\).

(II). Dựng góc \(\widehat {xOy} = {70^o}\).

(III). Vẽ tia OM, đó là tia phân giác của góc xOy cần dựng.

(IV). Dựng cung tròn tâm O bán kính tuỳ ý; cắt Ox, Oy lần lượt tại A và B.

Sắp xếp nào sau đây đúng?

A. (II) – (IV) – (I) – (III);

B. (II) – (I) – (III) – (IV);

C. (I) – (IV) – (II) – (III);

D. (I) – (III) – (II) – (IV).

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 7

Xét bài toán: "Cho \(\widehat {aOc} = {140^o}\). Nêu cách dựng tia phân giác của \(\widehat {aOc}\) bằng thước đo góc". Hãy sắp xếp một cách hợp lý các câu sau đây để có lời giải của bài toán trên.

(I). Tính \(\frac{{\widehat {aOc}}}{2} = \frac{{{{140}^o}}}{2} = {70^o}\).

(II). Dùng thước nối từ đỉnh của góc tới điểm đã đánh dấu ta được tia phân giác.

(III). Đặt tâm của thước đo góc trùng với đỉnh O sao cho một cạnh của thước đo trùng với cạnh Oc.

(IV). Dựng góc \(\widehat {aOc} = {140^o}\).

(V). Đánh dấu điểm chỉ vạch 70°.

Sắp xếp nào sau đây đúng?

A. (III) – (V) – (I) – (II) – (IV);

B. (III) – (I) – (V) – (II) – (IV);

C. (IV) – (III) – (I) – (V) – (II);

D. (IV) – (III) – (I) – (II) – (V).

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Xem thêm các câu hỏi khác »

Hỏi bài tập

Đăng ký gói thi VIP

VIP +1 tháng ( 199,000 VNĐ )

VIP +1 - Luyện thi tất cả các đề có trên Website trong 1 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +3 tháng ( 299,000 VNĐ )

VIP +3 - Luyện thi tất cả các đề có trên Website trong 3 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +6 tháng ( 399,000 VNĐ )

VIP +6 - Luyện thi tất cả các đề có trên Website trong 6 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +12 tháng ( 499,000 VNĐ )

VIP +12 - Luyện thi tất cả các đề có trên Website trong 12 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

Tia Am là phân giác của \(\widehat {bAc}\) nếu:

Bình luận

Cho tia Ob nằm giữa hai tia Oa và Oc; \(\widehat {aOb} = \widehat {bOc} = {20^o}\). Khẳng định nào sau đây sai?

Tia Ob là phân giác của \(\widehat {aOc}\) trong hình vẽ nào dưới đây?

Cho hình vẽ sau và cho biết tia OC là tia phân giác của góc nào?

Cho hình vẽ sau: Tia Oy là tia phân giác của góc nào?

Quan sát hình vẽ sau và cho biết tia Ob có là tia phân giác của \(\widehat {aOc}\) không? Vì sao?

VIP +1 tháng ( 199,000 VNĐ )

VIP +3 tháng ( 299,000 VNĐ )

VIP +6 tháng ( 399,000 VNĐ )

VIP +12 tháng ( 499,000 VNĐ )

🔥 Đề thi HOT:

CHỌN BỘ SÁCH BẠN MUỐN XEM

Đăng ký

Đăng nhập

Quên mật khẩu

Cho hình vẽ sau:

Tia Oy là tia phân giác của góc nào?