Câu hỏi:
09/08/2022 594
Cho góc bẹt \(\widehat {aOb}\). Gọi Oc là tia phân giác của \(\widehat {aOb}\); Ox là phân giác của \(\widehat {aOc}\); Oy là phân giác của \(\widehat {cOb}\). Số đo \(\widehat {xOy}\) là:
Quảng cáo
Trả lời:
Giải bởi Vietjack
Hướng dẫn giải:
Đáp án đúng là: A
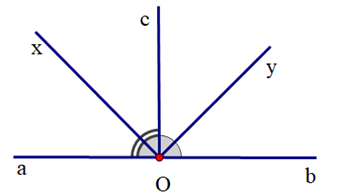
Vì Oc là tia phân giác của \(\widehat {aOb}\) nên \(\widehat {aOc} = \widehat {cOb} = \frac{1}{2}\widehat {aOb}\).
Suy ra \(\widehat {aOc} = \widehat {cOb} = \frac{1}{2}{.180^o} = {90^o}\) (vì \(\widehat {aOb}\) là góc bẹt)
Vì Ox là phân giác của \(\widehat {aOc}\) nên:
\(\widehat {xOc} = \frac{1}{2}\widehat {aOc} = \frac{1}{2}{.90^o} = {45^o}\).
Vì Oy là phân giác của \(\widehat {cOb}\) nên:
\(\widehat {cOy} = \frac{1}{2}\widehat {cOb} = \frac{1}{2}{.90^o} = {45^o}\).
Ta có tia Oc nằm giữa hai tia Ox và Oy nên:
\(\widehat {xOy} = \widehat {xOc} + \widehat {cOy} = {45^o} + {45^o} = {90^o}\).
Vậy \(\widehat {xOy} = {90^o}\).
Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Hướng dẫn giải:
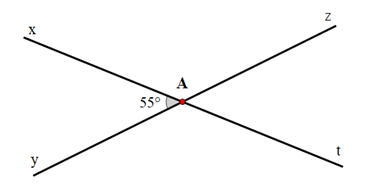
Suy ra \[\widehat {xAz} = {180^o} - \widehat {xAy} = {180^o} - {55^o} = {125^o}\];
Lời giải
Hướng dẫn giải:
Đáp án đúng là: B
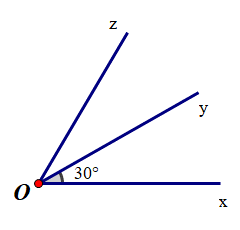
Vì Oy là tia phân giác \(\widehat {xOz}\) nên \(\widehat {xOy} = \frac{{\widehat {xOz}}}{2}\).
Suy ra \(\widehat {xOz} = 2.\widehat {xOy} = {2.30^o} = {60^o}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
Đề kiểm tra cuối học kỳ 2 Toán 7 Kết nối tri thức có đáp án - Đề 1
-
Bộ 7 đề thi học kì 2 Toán lớp 7 Chân trời sáng tạo có đáp án - Đề 04
-
15 câu Trắc nghiệm Toán 7 Kết nối tri thức Bài 1: Tập hợp các số hữu tỉ có đáp án
-
Đề kiểm tra cuối học kỳ 2 Toán 7 Kết nối tri thức có đáp án - Đề 2
-
Bộ 7 đề thi học kì 2 Toán lớp 7 Chân trời sáng tạo có đáp án - Đề 01
-
15 câu Trắc nghiệm Toán 7 Cánh diều Bài 1: Tập hợp Q các số hữu tỉ có đáp án
-
Bộ 15 đề thi Học kì 2 Toán 7 có đáp án (Mới nhất) - đề 2
-
15 câu Trắc nghiệm Toán 7 Chân trời sáng tạo Bài 1: Tập hợp các số hữu tỉ có đáp án