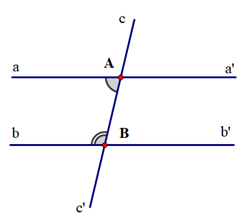
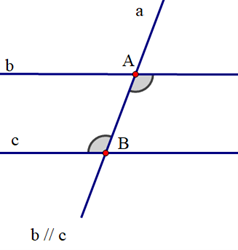
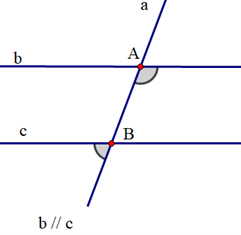
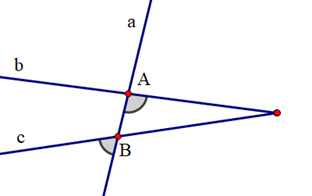
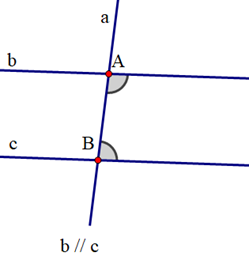
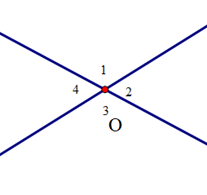
Cho định lí: “Hai tia phân giác của hai góc kề bù thì vuông góc với nhau” được minh hoạ bởi hình vẽ sau:
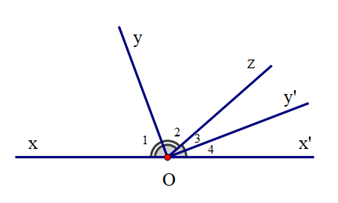
Hãy sắp xếp các câu sau để được lời giải hoàn chỉnh cho bài toán chứng minh định lí trên:
(I). “Suy ra Oy vuông góc với Oy'
Vậy định lí được chứng minh.”;
(II). “Vì Oy' là tia phân giác của \(\widehat {x'Oz}\) (giả thiết) nên \({\widehat O_3} = \frac{1}{2}\widehat {x'Oz}\)”;
(III) “Mà \(\widehat {xOz}\) và \(\widehat {zOx'}\)là hai góc kề bù (giả thiết)
Nên \(\widehat {xOz} + \widehat {zOx'} = 180^\circ \) (tính chất hai góc kề bù)
Do đó \(\widehat {yOy'} = \frac{1}{2}{.180^o} = {90^o}\)”;
(IV). “Có \(\widehat {yOy'} = {\widehat O_2} + {\widehat O_3}\)\( = \frac{1}{2}\widehat {xOz} + \frac{1}{2}\widehat {x'Oz}\)\( = \frac{1}{2}\left( {\widehat {xOz} + \widehat {zOx'}} \right)\)”
(V). “Vì Oy là tia phân giác của \(\widehat {xOz}\)(giả thiết) nên \({\widehat O_2} = \frac{1}{2}\widehat {xOz}\)”.
Quảng cáo
Trả lời:
Giải bởi Vietjack
Hướng dẫn giải:
Đáp án đúng là: B
Để chứng minh định lí trên, ta làm như sau:
Vì Oy là tia phân giác của \(\widehat {xOz}\)(giả thiết) nên \({\widehat O_2} = \frac{1}{2}\widehat {xOz}\)
Vì Oy' là tia phân giác của \(\widehat {x'Oz}\) (giả thiết) nên \({\widehat O_3} = \frac{1}{2}\widehat {x'Oz}\)
Có \(\widehat {yOy'} = {\widehat O_2} + {\widehat O_3}\)\( = \frac{1}{2}\widehat {xOz} + \frac{1}{2}\widehat {x'Oz}\)\( = \frac{1}{2}\left( {\widehat {xOz} + \widehat {zOx'}} \right)\)
Mà \(\widehat {xOz}\) và \(\widehat {zOx'}\)là hai góc kề bù (giả thiết)
Nên \(\widehat {xOz} + \widehat {zOx'} = 180^\circ \) (tính chất hai góc kề bù)
Do đó \(\widehat {yOy'} = \frac{1}{2}{.180^o} = {90^o}\)
Suy ra Oy vuông góc với Oy'
Vậy định lí được chứng minh.
Vậy ta sắp xếp các bước như sau: (V) – (II) – (IV) – (III) – (I).
Ta chọn phương án B.
Hot: Giáo án năng lực số, PPT AI khởi động lớp 1-12 (Update 2026) (chỉ từ 150k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
A.
|
GT |
x ⊥ y; y // z |
|
KL |
x ⊥ z |
B.
|
GT |
x // y; y // z |
|
KL |
x ⊥ z |
C.
|
GT |
x ⊥ y; y ⊥ z |
|
KL |
x // z |
D.
|
GT |
x ⊥ y; y // z |
|
KL |
x // z |
Lời giải
Hướng dẫn giải:
Đáp án đúng là: A
Giả thiết là: một đường thẳng vuông góc với một trong hai đường thẳng song song.
Kết luận là: đường thẳng đó vuông góc với đường thẳng còn lại.
Ta có thể viết giả thiết và kết luận của định lí trên bằng kí hiệu như sau:
|
GT |
x \( \bot \) y; y // z |
|
KL |
x \( \bot \) z |
Lời giải
Hướng dẫn giải:
Đáp án đúng là: A
Hình A cho thấy đường thẳng a cắt hai đường thẳng song song b và c và hai góc ở vị trí so le trong bằng nhau.
Do đó hình A minh hoạ cho định lí: “Một đường thẳng cắt hai đường thẳng song song thì hai góc so le trong bằng nhau”.
Hình B kí hiệu góc tại đỉnh A và đỉnh B không phải là hai góc so le trong. Do đó B sai.
Hình C vẽ hai đường thẳng b và c không song song với nhau. Do đó C sai.
Hình D kí hiệu góc tại đỉnh A và đỉnh B không phải là hai góc so le trong. Do đó D sai.
Vậy ta chọn phương án A.
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A.
|
GT |
\({\widehat O_1}\) và \({\widehat O_3}\) là hai góc đối đỉnh |
|
KL |
\({\widehat O_1} + {\widehat O_3} = 180^\circ \) |
B.
|
GT |
\({\widehat O_1}\) và \({\widehat O_3}\) là hai góc kề bù |
|
KL |
\({\widehat O_1} = {\widehat O_3}\) |
C.
|
GT |
\({\widehat O_1}\) và \({\widehat O_3}\) là hai góc đối đỉnh |
|
KL |
\({\widehat O_1} = {\widehat O_3}\) |
D.
|
GT |
\({\widehat O_1}\) và \({\widehat O_3}\) là hai góc kề bù |
|
KL |
\({\widehat O_3} = {\widehat O_4}\) |
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A.
|
GT |
aa' cắt cc' tại A, bb' cắt cc' tại B, aa' ≠ bb', \[\widehat {aAB} = \widehat {bBc'}\] |
|
KL |
\[\widehat {{\rm{aA}}B} + \widehat {ABb} = 180^\circ ;\] \[\widehat {{\rm{a'A}}B} + \widehat {ABb'} = 180^\circ \] |
B.
|
GT |
aa' cắt cc' tại A, bb' cắt cc' tại B, aa' ≠ bb' |
|
KL |
\[\widehat {aAB} = \widehat {bBc'};\] \[\widehat {{\rm{aA}}B} + \widehat {ABb} = 180^\circ ;\] \[\widehat {{\rm{a'A}}B} + \widehat {ABb'} = 180^\circ \] |
C.
|
GT |
aa' cắt cc' tại A, bb' cắt cc' tại B, aa' ≠ bb', \[\widehat {aAB} = \widehat {bBc'};\] \[\widehat {{\rm{aA}}B} + \widehat {ABb} = 180^\circ ;\] |
|
KL |
\[\widehat {{\rm{a'A}}B} + \widehat {ABb'} = 180^\circ \] |
D.
|
GT |
aa' cắt cc' tại A, bb' cắt cc' tại B, aa' ≠ bb', \[\widehat {aAB} = \widehat {bBc'};\] |
|
KL |
\[\widehat {{\rm{aA}}B} = \widehat {ABb};\] \[\widehat {{\rm{a'A}}B} = \widehat {ABb'};\] |
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập