16 Bài tập Cách viết giả thiết, kết luận, vẽ hình và chứng minh một định lí (có lời giải)
76 người thi tuần này 4.6 753 lượt thi 16 câu hỏi 30 phút
🔥 Đề thi HOT:
15 câu Trắc nghiệm Toán 7 Kết nối tri thức Bài 1: Tập hợp các số hữu tỉ có đáp án
22.3 K lượt thi
15 câu hỏi
Bài tập: Hai tam giác bằng nhau có đáp án
6.7 K lượt thi
14 câu hỏi
Bài tập: Giá trị của một biểu thức đại số có đáp án
5.8 K lượt thi
10 câu hỏi
Bài tập Trắc nghiệm Chương 3 Hình học 7 có đáp án
5.5 K lượt thi
24 câu hỏi
Bài tập: Quan hệ giữa ba cạnh của một tam giác. Bất đẳng thức tam giác có đáp án
5.4 K lượt thi
10 câu hỏi
Bài tập: Trường hợp bằng nhau thứ nhất của tam giác: cạnh - cạnh - cạnh có đáp án
6.9 K lượt thi
16 câu hỏi
Bài tập: Các góc tạo bởi một đường thẳng cắt hai đường thẳng có đáp án
6.1 K lượt thi
15 câu hỏi
Bài tập: Tính chất ba đường phân giác của tam giác có đáp án
6 K lượt thi
10 câu hỏi
Nội dung liên quan:
Danh sách câu hỏi:
Lời giải
Hướng dẫn giải:
|
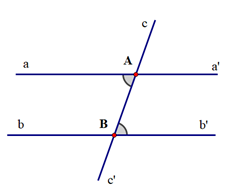
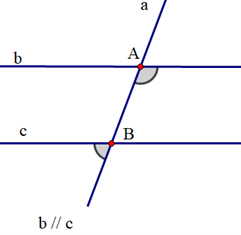
GT |
aa' cắt cc’ tại A; bb' cắt cc’ tại B; \[\widehat {aAB} = \widehat {ABb'}\] |
|
KL |
\[\widehat {cAa'} = \widehat {ABb'}\] \[\widehat {aAB} = \widehat {bBc'}\] \[\widehat {aAc} = \widehat {bBA}\] \[\widehat {a'AB} = \widehat {b'Bc'}\] |
Lời giải
Hướng dẫn giải:
+ Ta có \[\widehat {aAB} = \widehat {ABb'}\] (giả thiết)
Mà \[\widehat {aAB} = \widehat {cAa'}\] (hai góc đối đỉnh)
Suy ra \[\widehat {cAa'} = \widehat {ABb'}\] (vì cùng bằng \[\widehat {aAB}\]).
+ Ta có \[\widehat {aAB} = \widehat {ABb'}\](giả thiết)
Mà \[\widehat {ABb'} = \widehat {bBc'}\] (hai góc đối đỉnh)
Suy ra \[\widehat {aAB} = \widehat {bBc'}\] (vì cùng bằng \[\widehat {ABb'}\]).
+ Ta có \[\widehat {aAc}\] + \[\widehat {BAa}\] = 180° (hai góc kề bù)
Và \[\widehat {bBA}\] + \[\widehat {ABb'}\] = 180° (hai góc kề bù)
Mà \[\widehat {aAB} = \widehat {ABb'}\]
Suy ra \[\widehat {aAc}\] = \[\widehat {bBA}\].
+ Ta có \[\widehat {a'AB}\] = \[\widehat {aAc}\] (hai góc đối đỉnh)
\[\widehat {b'Bc'}\] = \[\widehat {bBA}\] (hai góc đối đỉnh)
Mà \[\widehat {aAc}\] = \[\widehat {bBA}\]
Suy ra \[\widehat {a'AB} = \widehat {b'Bc'}\].
Vậy định lí được chứng minh.
Lời giải
Hướng dẫn giải:
|
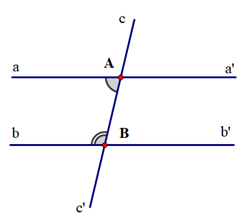
GT |
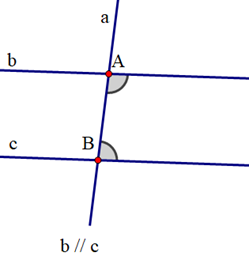
aa' cắt cc’ tại A; bb' cắt cc’ tại B; aa’ // bb’ |
|
KL |
\[\widehat {aAB} + \widehat {ABb} = 180^\circ ;\] \[\widehat {a'AB} + \widehat {ABb'} = 180^\circ \] |
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A.
|
GT |
x ⊥ y; y // z |
|
KL |
x ⊥ z |
B.
|
GT |
x // y; y // z |
|
KL |
x ⊥ z |
C.
|
GT |
x ⊥ y; y ⊥ z |
|
KL |
x // z |
D.
|
GT |
x ⊥ y; y // z |
|
KL |
x // z |
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 8
A. Nếu hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thứ ba thì chúng song song với nhau;
B. Nếu một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó vuông góc với đường thẳng còn lại;
C. Nếu hai đường thẳng phân biệt cùng song song với một đường thẳng thứ ba thì chúng song song với nhau;
D. Cả A, B, C đều sai.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 9
A. Nếu hai đường thẳng song song với nhau thì chúng vuông góc với một đường thẳng thứ ba;
B. Nếu hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thứ ba thì chúng vuông góc với nhau;
C. Nếu một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó song song với đường thẳng còn lại;
D. Nếu hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thứ ba thì chúng song song với nhau.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 10
A.
|
GT |
aa' cắt cc' tại A, bb' cắt cc' tại B, aa' ≠ bb', \[\widehat {aAB} = \widehat {bBc'}\] |
|
KL |
\[\widehat {{\rm{aA}}B} + \widehat {ABb} = 180^\circ ;\] \[\widehat {{\rm{a'A}}B} + \widehat {ABb'} = 180^\circ \] |
B.
|
GT |
aa' cắt cc' tại A, bb' cắt cc' tại B, aa' ≠ bb' |
|
KL |
\[\widehat {aAB} = \widehat {bBc'};\] \[\widehat {{\rm{aA}}B} + \widehat {ABb} = 180^\circ ;\] \[\widehat {{\rm{a'A}}B} + \widehat {ABb'} = 180^\circ \] |
C.
|
GT |
aa' cắt cc' tại A, bb' cắt cc' tại B, aa' ≠ bb', \[\widehat {aAB} = \widehat {bBc'};\] \[\widehat {{\rm{aA}}B} + \widehat {ABb} = 180^\circ ;\] |
|
KL |
\[\widehat {{\rm{a'A}}B} + \widehat {ABb'} = 180^\circ \] |
D.
|
GT |
aa' cắt cc' tại A, bb' cắt cc' tại B, aa' ≠ bb', \[\widehat {aAB} = \widehat {bBc'};\] |
|
KL |
\[\widehat {{\rm{aA}}B} = \widehat {ABb};\] \[\widehat {{\rm{a'A}}B} = \widehat {ABb'};\] |
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 11
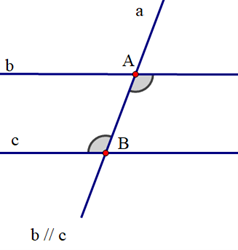
Cho hình vẽ:
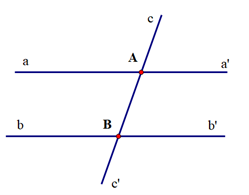
Bảng sau là giả thiết, kết luận của định lí nào?
|
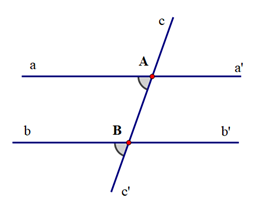
GT |
aa' cắt cc' tại A, bb' cắt cc' tại B (aa' ≠ bb') \[\widehat {aAB}\] + \[\widehat {ABb}\] = 180° |
|
KL |
\[\widehat {aAB} = \widehat {ABb'};\]\[\widehat {a'AB} = \widehat {ABb}\] |
A. Nếu hai đường thẳng phân biệt cùng cắt đường thẳng thứ ba và trong các góc tạo thành có một cặp góc đồng vị bằng nhau thì các cặp góc trong cùng phía bù nhau.
B. Nếu hai đường thẳng phân biệt cùng cắt đường thẳng thứ ba và trong các góc tạo thành có một cặp góc trong cùng phía bù nhau thì các cặp góc đồng vị bằng nhau.
C. Nếu hai đường thẳng phân biệt cùng cắt đường thẳng thứ ba và trong các góc tạo thành có một cặp góc trong cùng phía bù nhau thì các cặp góc so le trong bằng nhau.
D. Nếu hai đường thẳng phân biệt cùng cắt đường thẳng thứ ba và trong các góc tạo thành có một cặp góc đồng vị bằng nhau thì các cặp góc so le trong bằng nhau.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 12
A. “Hai đường thẳng phân biệt cùng song song với một đường thẳng thứ ba thì chúng song song với nhau”;
B. “Nếu hai đường thẳng phân biệt cùng cắt đường thẳng thứ ba và trong các góc tạo thành có một cặp góc đồng vị bằng nhau thì chúng song song với nhau”;
C. “Hai góc có tổng bằng 180° thì bù với nhau”;
D. “Nếu hai đường thẳng cắt nhau và trong các góc tạo thành có một góc bằng 90° thì vuông góc với nhau”.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 13
A. (II) – (III) – (I) – (IV) – (V);
B. (V) – (II) – (IV) – (III) – (I);
C. (IV) – (II) – (V) – (I) – (III);
D. (IV) – (III) – (II) – (V) – (I).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 14
A.
|
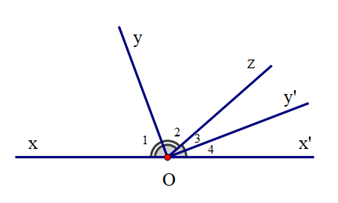
GT |
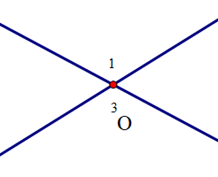
\({\widehat O_1}\) và \({\widehat O_3}\) là hai góc đối đỉnh |
|
KL |
\({\widehat O_1} + {\widehat O_3} = 180^\circ \) |
B.
|
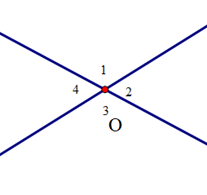
GT |
\({\widehat O_1}\) và \({\widehat O_3}\) là hai góc kề bù |
|
KL |
\({\widehat O_1} = {\widehat O_3}\) |
C.
|
GT |
\({\widehat O_1}\) và \({\widehat O_3}\) là hai góc đối đỉnh |
|
KL |
\({\widehat O_1} = {\widehat O_3}\) |
D.
|
GT |
\({\widehat O_1}\) và \({\widehat O_3}\) là hai góc kề bù |
|
KL |
\({\widehat O_3} = {\widehat O_4}\) |
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 15
A. (I) – (III) – (II) – (IV);
B. (II) – (III) – (I) – (IV);
C. (II) – (I) – (IV) – (III);
D. (II) – (III) – (IV) – (I);
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo