5 câu Trắc nghiệm Các trường hợp bằng nhau của tam giác vuông có đáp án (Nhận biết)
38 người thi tuần này 4.6 2.3 K lượt thi 5 câu hỏi 30 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Bộ 10 đề thi cuối kì 2 Toán 7 Cánh diều có đáp án - Đề 10
Bộ 10 đề thi cuối kì 2 Toán 7 Cánh diều có đáp án - Đề 9
Bộ 10 đề thi cuối kì 2 Toán 7 Cánh diều có đáp án - Đề 8
Bộ 10 đề thi cuối kì 2 Toán 7 Cánh diều có đáp án - Đề 7
Bộ 10 đề thi cuối kì 2 Toán 7 Cánh diều có đáp án - Đề 6
Bộ 10 đề thi cuối kì 2 Toán 7 Cánh diều có đáp án - Đề 5
Bộ 10 đề thi cuối kì 2 Toán 7 Cánh diều có đáp án - Đề 4
Bộ 10 đề thi cuối kì 2 Toán 7 Cánh diều có đáp án - Đề 3
Danh sách câu hỏi:
Câu 1
A. cạnh huyền – cạnh góc vuông;
B. cạnh huyền – góc nhọn;
C. cạnh – góc – cạnh;
Lời giải
Hướng dẫn giải
Đáp án đúng là: C
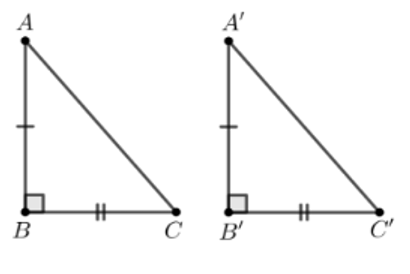
Xét ∆ABC và ∆DEF, có:
.
AB = DE (giả thiết)
BC = EF (giả thiết)
Do đó ∆ABC = ∆DEF (c.g.c)
Vậy ta chọn phương án C.
Lời giải
Hướng dẫn giải
Đáp án đúng là: D
⦁ Xét phương án A:
Xét ∆ABC và ∆A’B’C’, có:
.
AB = A’B’ (giả thiết)
BC = B’C’ (giả thiết)
Do đó ∆ABC = ∆A’B’C’ (c.g.c)
Vì vậy phương án A có chứa hai tam giác vuông bằng nhau.
⦁ Xét phương án B:
Xét ∆A’B’C’ và ∆ABC, có:
.
B’C’ = BC (giả thiết)
(giả thiết)
Do đó ∆A’B’C’ = ∆ABC (g.c.g)
Vì vậy phương án B có chứa hai tam giác vuông bằng nhau.
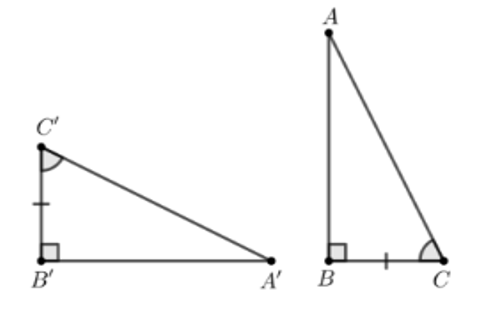
⦁ Xét phương án C:
Xét ∆ABC và ∆A’B’C’, có:
.
AC = A’C’ (giả thiết)
(giả thiết)
Do đó ∆ABC = ∆A’B’C’ (cạnh huyền – góc nhọn)
Vì vậy phương án C có chứa hai tam giác vuông bằng nhau.
⦁ Xét phương án D:
Xét ∆ABC và ∆A’B’C’, có:
.
(giả thiết)
(giả thiết)
Do đó ∆ABC và ∆A’B’C’ không bằng nhau do không có trường hợp bằng nhau góc – góc – góc.
Vậy ta chọn phương án D.
Câu 3
A. MN = XY;
B. MN = YZ;
C. ;
Lời giải
Hướng dẫn giải
Đáp án đúng là: A
Ta thấy MP, XZ lần lượt là cạnh góc vuông của ∆MNP và ∆XYZ.
Do đó để ∆MNP = ∆XYZ theo trường hợp cạnh huyền – cạnh góc vuông thì cần thêm điều kiện hai cạnh huyền của hai tam giác đó bằng nhau. Nghĩa là, MN = XY.
Vậy ta chọn phương án A.
Câu 4
A. ;
B. , AB = PQ, ;
C. , BC = QR, ;
Lời giải
Hướng dẫn giải
Đáp án đúng là: A
⦁ Xét phương án A:
Xét ∆ABC và ∆PQR, có:
.
(giả thiết)
(giả thiết)
Do đó ∆ABC và ∆PQR không bằng nhau do không có trường hợp góc – góc – góc.
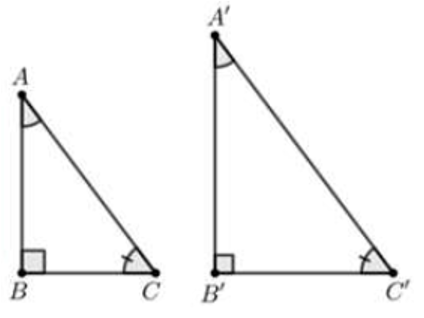
⦁ Xét phương án B:
Xét ∆ABC và ∆PQR, có:
.
AB = PQ (giả thiết)
(giả thiết)
Do đó ∆ABC = ∆PQR (g.c.g).
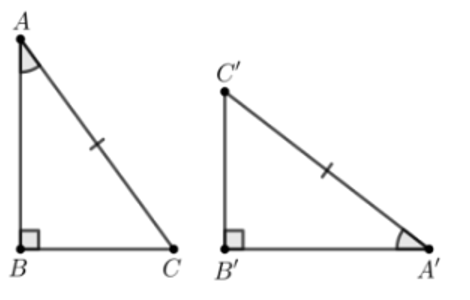
⦁ Xét phương án C:
Xét ∆ABC và ∆PQR, có:
.
BC = QR (giả thiết)
(giả thiết)
Do đó ∆ABC = ∆PQR (cạnh huyền – góc nhọn)
⦁ Xét phương án D:
Xét ∆ABC và ∆PQR, có:
.
BC = QR (giả thiết)
AC = PR (giả thiết)
Do đó ∆ABC = ∆PQR (cạnh huyền – cạnh góc vuông)
Vậy ta chọn phương án A.
Câu 5
A. Nếu hai cạnh góc vuông của tam giác vuông này lần lượt bằng hai cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đó bằng nhau;
B. Nếu cạnh huyền và một cạnh góc vuông của tam giác vuông này bằng cạnh huyền và một cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đó bằng nhau;
C. Nếu cạnh huyền và một góc nhọn của tam giác vuông này bằng cạnh huyền và một góc nhọn của tam giác vuông kia thì hai tam giác vuông đó bằng nhau;
Lời giải
Hướng dẫn giải
Đáp án đúng là: D
Phương án A: Phát biểu của trường hợp cạnh góc vuông – góc nhọn kề (hay g.c.g).
Phương án B: Phát biểu của trường hợp cạnh huyền – cạnh góc vuông.
Phương án C: Phát biểu của trường hợp cạnh huyền – góc nhọn.
Vậy ta chọn phương án D.