10 Bài tập Sử dụng tính chất trực tâm của tam giác để chứng minh hai đường thẳng vuông góc, ba đường thẳng đồng quy (có lời giải)

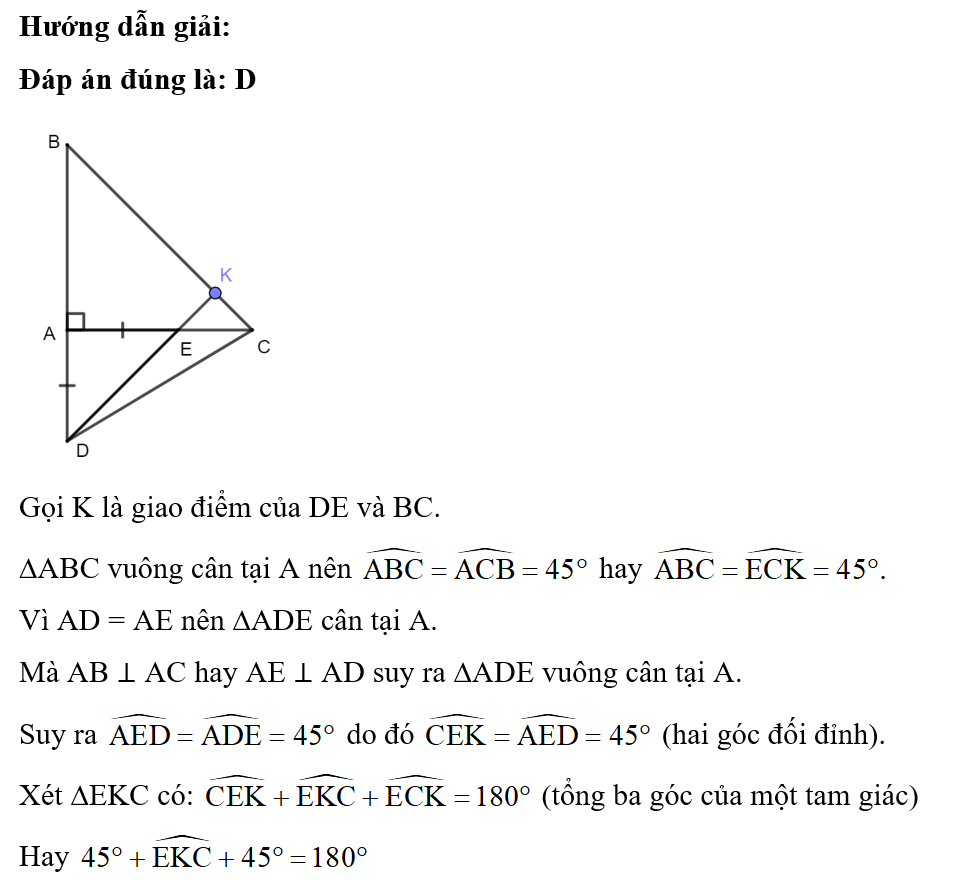
Hướng dẫn giải:

Đáp án đúng là: C

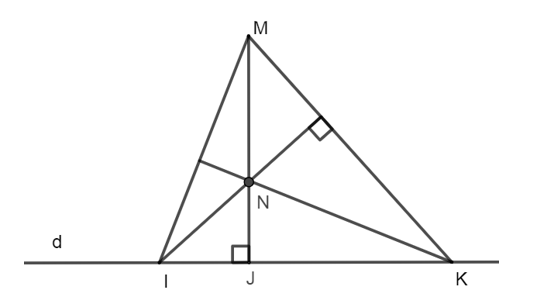
Ta có: MJ ⊥ IK tại J nên MJ là đường cao của ∆MIK.

Mà N nằm trên đường thẳng qua I và vuông góc với MK nên IN ⊥ MK.

Do đó IN là đường cao của ΔMIK.

Xét ∆MIK có hai đường cao IN và MJ cắt nhau tại N nên N là trực tâm của ΔMIK.

Suy ra KN là đường cao của ∆MIK hay KN ⊥ MI.

Hướng dẫn giải:

Đáp án đúng là: D

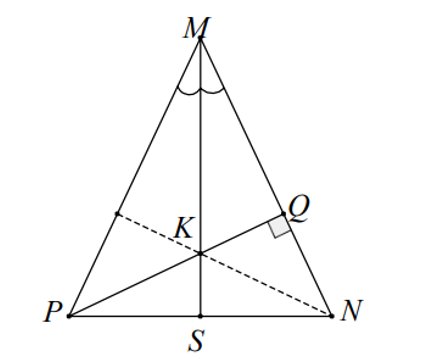
Xét ∆MPN cân tại M có MS là đường phân giác (giả thiết) nên MS đồng thời là đường cao. Suy ra MS ⊥ PN

∆MPN có MS ⊥ PN, PQ ⊥ MN và MS cắt PQ tại K nên K là trực tâm của ∆MPN.

Do đó NK ⊥ MP.

Vậy cả A, B, C đều là khẳng định đúng. Ta chọn phương án D.

Hướng dẫn giải:

Đáp án đúng là:D

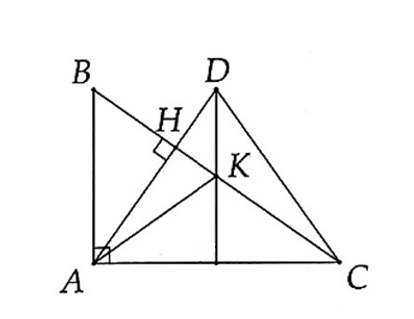
Vì AB ⊥ AC và DK // AB nên DK ⊥ AC.

Xét ∆ADC có: DK ⊥ AC, CH ⊥ AD và DK cắt CH tại K nên K là trực tâm ∆ADC.

Suy ra AK ⊥ CD và ba đường thẳng AK, DK, BC đồng quy.

Vậy cả A, B, C đều là khẳng định đúng. Ta chọn phương án D.

Hướng dẫn giải:

Đáp án đúng là: D

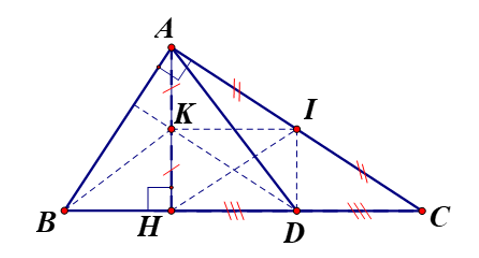
⦁ Trong ∆AHC vuông tại H, dễ dàng chứng minh được $AI=CI=HI=\frac{1}{2}AC.$

Do đó I cách đều ba đỉnh của tam giác nên I là giao điểm ba trung trực của ∆AHC.

⦁ Ta có AH ⊥ BC, DI ⊥ BC suy ra AH // DI nên $\widehat{KDI}=\widehat{HKD}$ (so le trong);

AH ⊥ BC, IK ⊥ AK suy ra IK // BC nên $\widehat{HDK}=\widehat{IKD}$ (so le trong).

Xét ∆KHD và ∆DIK có:

$\widehat{HKD}=\widehat{KDI};$ KD là cạnh chung; $\widehat{HDK}=\widehat{IKD}$

Do đó ∆KHD = ∆DIK (g.c.g).

Suy ra HK = ID, HD = IK (các cặp cạnh tương ứng)

Xét ∆KDH (vuông tại H) và ∆ICD (vuông tại D) có:

HK = ID (chứng minh trên);

HD = DC (do DI là trung trực của HC).

Do đó ∆KDH = ∆IDC (hai cạnh góc vuông).

Suy ra $\widehat{KDH}=\widehat{ICD}$ (hai góc tương ứng)

Mà hai góc này ở vị trí đồng vị nên DK // AC.

Lại có AB ⊥ AC nên DK ⊥ AB

Trong ∆ABD có: AH ⊥ BD (giả thiết), DK ⊥ AB và AH cắt DK tại K

Do đó K là trực tâm ∆ABD, suy ra BK ⊥ AD.