Cho ∆MNP cân tại M, đường cao PQ cắt đường phân giác MS ở K. Khẳng định nào sau đây là sai?
Cho ∆MNP cân tại M, đường cao PQ cắt đường phân giác MS ở K. Khẳng định nào sau đây là sai?
A. NK ⊥ MP;
B. MK ⊥ NP;
C. K là trực tâm của tam giác MNP;
D. Cả A, B, C đều sai.
Quảng cáo
Trả lời:
Giải bởi Vietjack
Hướng dẫn giải:
Đáp án đúng là: D
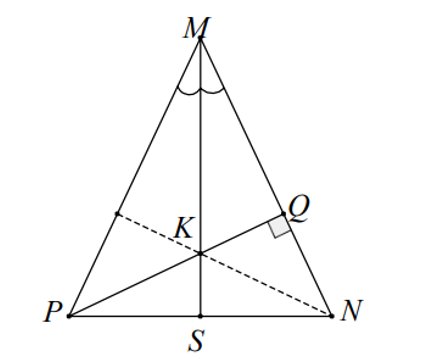
Xét ∆MPN cân tại M có MS là đường phân giác (giả thiết) nên MS đồng thời là đường cao. Suy ra MS ⊥ PN
∆MPN có MS ⊥ PN, PQ ⊥ MN và MS cắt PQ tại K nên K là trực tâm của ∆MPN.
Do đó NK ⊥ MP.
Vậy cả A, B, C đều là khẳng định đúng. Ta chọn phương án D.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
A. Chỉ (I) sai;
B. Chỉ (II) sai;
C. Cả (I), (II) đúng;
D. Cả (I), (II) sai.
Lời giải
Hướng dẫn giải:
Đáp án đúng là: C
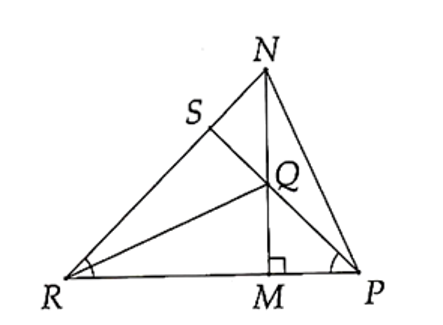
ΔMPQ vuông tại M có MQ = MP nên là tam giác vuông cân tại M, do đó
Suy ra (đối đỉnh)
Tương tự, ΔMNR vuông cân tại M có
Trong ΔNSQ có: và
Do đó nên QS ⊥ NS hay PS ⊥ NR.
Trong ΔNPR có các đường cao PS và MN cắt nhau tại Q.
Suy ra Q là trực tâm ΔNPR.
Ta có: MN, PS và RQ là ba đường cao của tam giác NPR nên đồng quy tại Q.
Câu 2
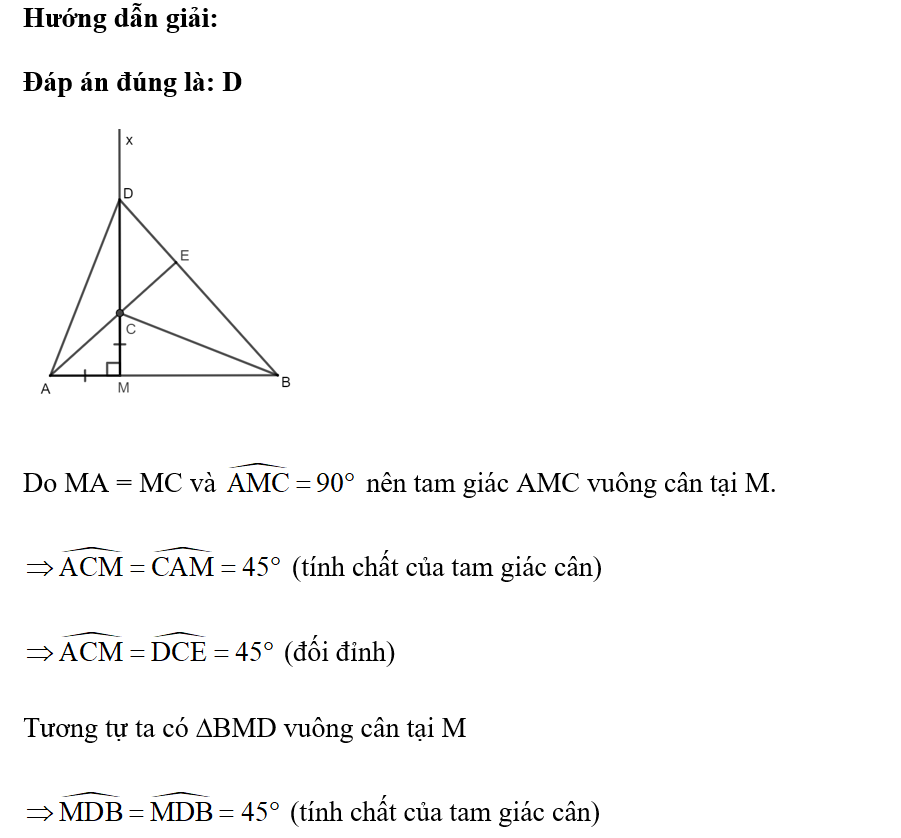
A. Ba đường AE, DM và BC đồng quy tại C;
B. AE ⊥ BD;
C. BC ⊥ AD;
D. Cả A, B, C đều là khẳng định sai.
Lời giải
Câu 3
A. I là giao điểm ba trung trực của ∆AHC;
B. KD // AC;
C. BK ⊥ AD;
D. Cả A, B, C đều sai.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. DK ⊥ AC;
B. AK ⊥ BD;
C. AK, DK, BC đồng quy;
D. Cả A, B, C đều đúng.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. 3;
B. 2;
C. 1;
D. 0.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. AK ⊥ CD;
B. CH ⊥ AD;
C. DK ⊥ AC.
D. Cả A, C đều sai.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập