Câu hỏi:
06/10/2022 160Có bao nhiêu số nguyên n thỏa mãn \[(2n - 1) \vdots (n + 1)\;?\]
Đáp án chính xác
Sách mới 2k7: Tổng ôn Toán, Lí, Hóa, Văn, Sử, Địa…. kỳ thi tốt nghiệp THPT Quốc gia 2025, đánh giá năng lực (chỉ từ 110k).
Quảng cáo
Trả lời:
Giải bởi Vietjack
Trả lời:
Ta có
\[2n - 1 = 2n + 2 - 3 = (2n + 2) - 3 = 2(n + 1) - 3\]
Vì \[\left( {2n - 1} \right) \vdots \left( {n + 1} \right)\] nên \[\left[ {2\left( {n + 1} \right) - 3} \right] \vdots \left( {n + 1} \right)\]
Mà \[2\left( {n + 1} \right) \vdots \left( {n + 1} \right)\] suy ra \[ - 3 \vdots \left( {n + 1} \right) \Rightarrow n + 1 \in U\left( { - 3} \right) = \left\{ { \pm 1;\, \pm 3} \right\}\]
Ta có bảng sau:
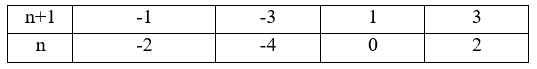
Vậy \[n \in \left\{ { - 4;\, - 2;\,0;\,2} \right\}\]
Do đó có 4 số nguyên nn thỏa mãn đề bài.
Đáp án cần chọn là: D
Nhà sách VIETJACK:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 2:
Cho các số sau: 1280;−291;43;−52;28;1;0 . Các số đã cho sắp xếp theo thứ tự giảm dần là:
Xem đáp án »
06/10/2022
369
Câu 4:
Tìm giá trị lớn nhất của biểu thức : \[C = - {\left( {x - 5} \right)^2} + 10\]
Xem đáp án »
06/10/2022
316
Câu 5:
Bỏ ngoặc rồi tính: \[\left( {52 - 69 + 17} \right) - \left( {52 + 17} \right)\;\] ta được kết quả là
Xem đáp án »
06/10/2022
315
Bình luận
🔥 Đề thi HOT:
-
Bài tập: Tập hợp. Phần tử của tập hợp chọn lọc, có đáp án
-
31 câu Trắc nghiệm Toán 6 KNTT Bài 1: Tập hợp có đáp án
-
Đề thi Toán lớp 6 Học kì 1 năm 2020 - 2021 cực hay, có đáp án (Đề 1)
-
Dạng 4: Một số bài tập nâng cao về lũy thừa
-
Xét tính chia hết của một tổng hoặc hiệu
-
Dạng 4. Quy tắc dấu ngoặc có đáp án
-
10 Bài tập Các bài toán thực tế về số nguyên âm (có lời giải)
-
Dạng 4. Thực hiện phép tính (tiếp theo) có đáp án
về câu hỏi!