Câu hỏi:

31/10/2022 503

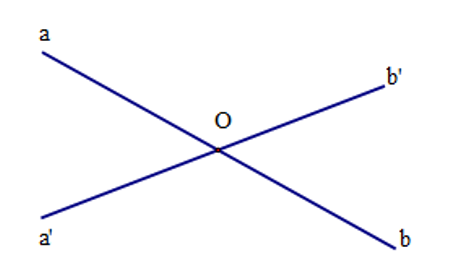
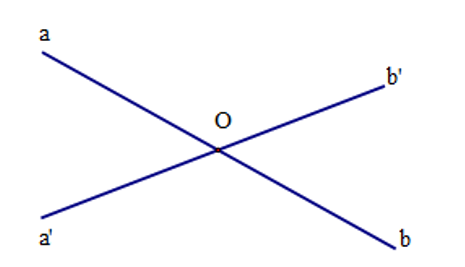
Cho giả thiết a // b, c cắt a tại A, cắt b tại B. Kết luận $\hat{cAa} = \hat{A B b}$ . Giả thiết và kết luận trên thể hiện định lí nào?

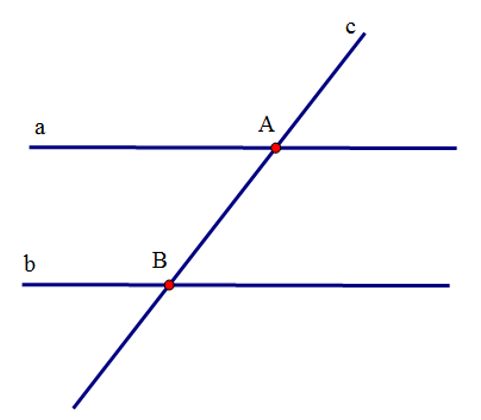
A. Nếu một đường thẳng cắt hai đường thẳng song song thì hai góc đồng vị bằng nhau;

B. Nếu một đường thẳng cắt hai đường thẳng song song thì hai góc so le trong bằng nhau;

C. Nếu một đường thẳng cắt hai đường thẳng thì hai góc đồng vị bằng nhau;

D. Nếu một đường thẳng cắt hai đường thẳng song song thì hai góc đồng vị bù nhau.

Câu hỏi trong đề: 15 câu Trắc nghiệm Toán 7 Kết nối tri thức Bài 11: Định lí và chứng minh định lí có đáp án (Phần 2) !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

Hướng dẫn giải

Đáp án đúng là: A

Ta thấy $\hat{cAa}$ và $\hat{ABb}$ là hai góc ở ở vị trí đồng vị. Theo tính chất hai đường thẳng song song, ta có $\hat{cAa}$ = $\hat{ABb}$ .

Vậy định lí: Nếu một đường thẳng cắt hai đường thẳng song song thì hai góc đồng vị bằng nhau.

Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Cho định lý: “ Nếu hai đường thẳng cùng song song với đường thẳng thứ ba thì hai đường thẳng song song”. Khi đó giả thiết và kết luận của định lí là:

A. GT: a // m, b // m. KL: a // b;

B. GT: a // m, b // m. KL: a $⊥$ b;

C. GT: a // m. KL: m // b;

D. GT: b // m. KL: a // m.

Lời giải

Hướng dẫn giải

Đáp án đúng là: A

Định lý: “ Nếu hai đường thẳng cùng song song với đường thẳng thứ ba thì hai đường thẳng song song” có GT – KL là:

GT: a // m, b // m. KL: a // b

Câu 2

Cho a // b. Khẳng định nào sau đây sai?

A. Nếu c $⊥$ a thì c $⊥$ b;

B. Nếu c // a thì c // b;

C. Nếu c $⊥$ a thì c // b;

D. Nếu c // b thì c // a.

Lời giải

Hướng dẫn giải

Đáp án đúng là: C

Định lí: Một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó cũng vuông góc với đường thẳng còn lại. Khẳng định A đúng.

Định lí: Một đường thẳng song song với một trong hai đường thẳng song song thì nó cũng song song với đường thẳng còn lại. Khẳng định B và D đúng.

Một đường thẳng vuông góc với một trong hai đường thẳng song song thì không song song với đường thẳng còn lại. Khẳng định C sai.

Vậy chọn đáp án C.

Câu 3

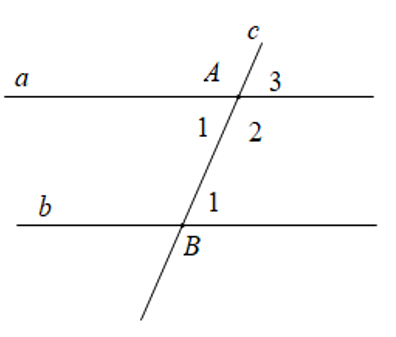
Cho giả thiết a // b, c cắt a tại A, cắt b tại B ( như hình vẽ ). Kết luận nào sau đây không hợp lí?

A. $\hat{A_{1}}$ = $\hat{B_{1}}$ ;

B. $\hat{A_{3}}$ = $\hat{B_{1}}$ ;

C. $\hat{A_{2}}$ = $\hat{A_{1}}$ ;

\hat{A_{3}}

\hat{A_{1}}

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 4

Cho định lí: “ Hai góc đối đỉnh thì bằng nhau ” như hình vẽ. Kết luận của định lí là:

A. ab $\cap$ a’b’ = { O };

B. $\hat{aOa'}$ = $\hat{bOb'}$ ;

C. ab $\cap$ a’b’ = { O }. $\hat{aOa'}$ = $\hat{bOb'}$ ;

D. Không đáp án nào đúng.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 5

Cho định lí: “ Hai góc đối đỉnh thì bằng nhau ” như hình vẽ. Giả thiết của định lí là:

A. ab giao a’b’ tại O, $\hat{aOa'}$ và $\hat{bOb'}$ là hai góc đối đỉnh;

B. $\hat{aOa'}$ = $\hat{bOb'}$ ;

C. ab giao a’b’ tại O, $\hat{aOa'}$ = $\hat{bOb'}$ ;

D. Không đáp án nào đúng.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 6

Cho giả thiết: c $⊥$ a , c $⊥$ b và a, b, c nằm trên cùng một mặt phẳng. Kết luận nào sau đây hợp lí?

A. a $⊥$ b;

B. a // b;

C. a cắt b;

D. Cả 3 đáp án trên đều sai.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Xem thêm các câu hỏi khác »

Cho giả thiết a // b, c cắt a tại A, cắt b tại B. Kết luận cAa^=ABb^. Giả thiết và kết luận trên thể hiện định lí nào?

Cho định lý: “ Nếu hai đường thẳng cùng song song với đường thẳng thứ ba thì hai đường thẳng song song”. Khi đó giả thiết và kết luận của định lí là:

Cho a // b. Khẳng định nào sau đây sai?

Cho giả thiết a // b, c cắt a tại A, cắt b tại B ( như hình vẽ ). Kết luận nào sau đây không hợp lí?

Cho định lí: “ Hai góc đối đỉnh thì bằng nhau ” như hình vẽ. Kết luận của định lí là:

Cho định lí: “ Hai góc đối đỉnh thì bằng nhau ” như hình vẽ. Giả thiết của định lí là:

Cho giả thiết: c ⊥ a , c ⊥ b và a, b, c nằm trên cùng một mặt phẳng. Kết luận nào sau đây hợp lí?

CHỌN BỘ SÁCH BẠN MUỐN XEM

Đăng ký

Đăng nhập

Quên mật khẩu

Cho giả thiết a // b, c cắt a tại A, cắt b tại B. Kết luận $\hat{cAa} = \hat{A B b}$ . Giả thiết và kết luận trên thể hiện định lí nào?

Cho giả thiết: c $⊥$ a , c $⊥$ b và a, b, c nằm trên cùng một mặt phẳng. Kết luận nào sau đây hợp lí?