Cho tam giác MNP có: MN < MP, MD ⊥ NP. Khẳng định nào sau đây là đúng
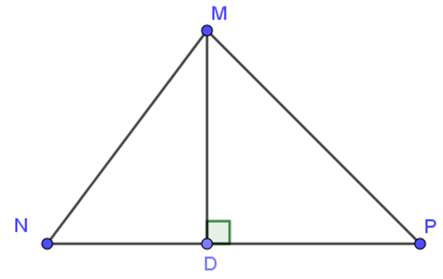

A. DN = DP;
B. MN = MP;
C. MD > MN;
D. MD < MP.
Câu hỏi trong đề: Đề kiểm tra giữa học kì 2 Toán lớp 7 CTST có đáp án !!
Quảng cáo
Trả lời:
Đáp án D
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Trên cùng một quãng đường, vận tốc và thời gian tỉ lệ nghịch với nhau.
Gọi v1, t1 lần lượt là vận tốc và thời gian của xe I; v2, t2 lần lượt là vận tốc và thời gian của xe II.
Thời gian xe I đi hết đoạn đường AB là:
14 – 8 = 6 (giờ).
Thời gian xe II đi hết đoạn đường AB là:
(14 – 0,5) – 9 = 4,5 (giờ).
Ta có \(\frac{{{v_1}}}{{{v_2}}}{\rm{ = }}\frac{{{t_2}}}{{{t_1}}} = \frac{{4,5}}{6} = \frac{3}{4}\) hay \(\frac{{{v_1}}}{3} = \frac{{{v_2}}}{4}\).
Vì vận tốc xe thứ hai lớn hơn vận tốc xe thứ nhất là 20 km/h nên v2 – v1 = 20.
Áp dụng tính chất dãy tỉ số bằng nhau, ta có:
\(\frac{{{v_1}}}{3} = \frac{{{v_2}}}{4} = \frac{{{v_2} - {v_1}}}{{4 - 3}} = \frac{{20}}{1} = 20\).
Suy ra v1 = 20 . 3 = 60; v2 = 20 . 4 = 80.
Vậy vận tốc của xe thứ nhất là 60 km/h, vận tốc của xe thứ hai là 80 km/h.
Lời giải
Đặt \(\frac{a}{b} = \frac{c}{d} = k\) suy ra a = bk, c = dk.
Ta có \(\frac{{a - 2b}}{b} = \frac{{bk - 2b}}{b} = \frac{{b\left( {k - 2} \right)}}{b} = k - 2\);
\(\frac{{c - 2d}}{d} = \frac{{dk - 2d}}{d} = \frac{{d\left( {k - 2} \right)}}{d} = k - 2\).
Vậy \(\frac{{a - 2b}}{b} = \frac{{c - 2d}}{d}\) (đpcm).
Câu 3
A. 12,5 : 34,5;
B. 29 : 65;
C. 25 : 69;
D. 1 : 3.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. –32;
B. 32;
C. –2;
D. 2.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.