Cho tam giác ABC cân tại A. Lấy điểm D trên cạnh AC, điểm E trên cạnh AC sao cho BD = CE.
Tìm vị trí của hai điểm D và E sao cho BD = DE = EC. Khi đó tìm vị trí của điểm I
Cho tam giác ABC cân tại A. Lấy điểm D trên cạnh AC, điểm E trên cạnh AC sao cho BD = CE.
Quảng cáo
Trả lời:
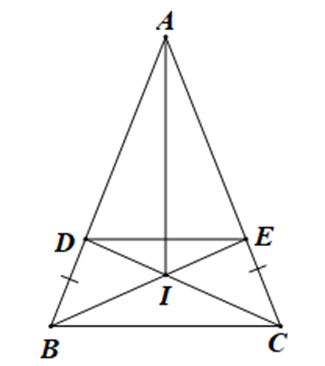
Xét DADE có AD = AE nên DADE cân tại A.
Suy ra \(\widehat {ADE} = \widehat {AED}\).
Mà \(\widehat {DAE} + \widehat {ADE} + \widehat {AED} = 180^\circ \) (tổng ba góc trong một tam giác)
Suy ra \(\widehat {ADE} = \widehat {AED} = \frac{{180^\circ - \widehat {DAE}}}{2}\,\,\,\,\,\left( 1 \right)\).
Tương tự với tam giác ABC cân tại A ta có \(\widehat {ABC} = \widehat {ACB} = \frac{{180^\circ - \widehat {BAC}}}{2}\,\,\,\,\,\left( 2 \right)\)
Từ (1) và (2) suy ra \(\widehat {ADE} = \widehat {ABC}\)
Mà hai góc này ở vị trí đồng vị nên DE // BC.
Suy ra \(\widehat {DEB} = \widehat {EBC}\) (hai góc so le trong) (3)
Do BD = DE nên DBDE là tam giác cân tại D
Suy ra \(\widehat {DBE} = \widehat {DEB}\) (4)
Từ (3) và (4) suy ra \(\widehat {DBE} = \widehat {EBC}\)
Khi đó BE là đường phân giác của góc ABC.
Tương tự, với DE = EC ta cũng chứng minh được CD là đường phân giác của góc ACB.
Xét tam giác ABC có BE, CE là hai đường phân giác của tam giác cắt nhau tại I
Suy ra I cách đều ba cạnh của tam giác ABC.
Vậy để BD = DE = EC thì BE và CD là hai đường phân giác của DABC, khi đó I cách đều ba cạnh của DABC.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Thực hiện phép chia đa thức như sau:
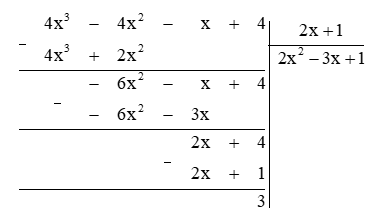
Do đó phép chia trên có thương là 2x2 – 3x + 1 và dư 3.
Để phép chia là phép chia hết thì 3 ⋮ (2x + 1), hay 2x + 1 ∈ Ư(3) = {1; –1; 3; –3}.
Ta có bảng sau:
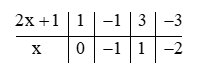
Vậy x ∈ {–2; –1; 0; 1}.
Lời giải
Bảng tỉ lệ phần trăm số tình nguyện viên tham gia của mỗi vùng miền trong đội tình nguyện viên đó:
|
Vùng miền |
Trung du và miền núi phía Bắc |
Đồng bằng sông Hồng |
Tây Nguyên |
Đồng bằng sông Cửu Long |
|
Tỉ lệ phần trăm |
12,5% |
30% |
20% |
37,5% |
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
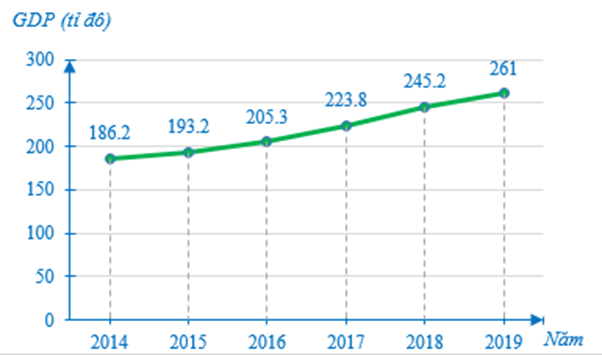
Câu 5
A. 130,5 tỉ đô la;
B. 132,5 tỉ đô la;
C. 134,5 tỉ đô la;
D. 136,5 tỉ đô la.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. \(P\left( F \right) = \frac{1}{{15}}\);
B. \(P\left( F \right) = \frac{2}{{15}}\);
C. \(P\left( F \right) = \frac{1}{5}\);
D. \(P\left( F \right) = \frac{1}{2}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A. x = 30° và tam giác ABC là tam giác cân
B. x = 40° và tam giác ABC là tam giác nhọn;
C. x = 80° và tam giác ABC là tam giác tù;
D. x = 90 và tam giác ABC là tam giác vuông.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.