Cho tam giác đều ABC cạnh bằng 2cm. Tính bán kính R của đường tròn ngoại tiếp tam giác ABC.
Cho tam giác đều ABC cạnh bằng 2cm. Tính bán kính R của đường tròn ngoại tiếp tam giác ABC.
A.
B.
C.
D.
Quảng cáo
Trả lời:
Giải bởi Vietjack
Đáp án C
Phương pháp
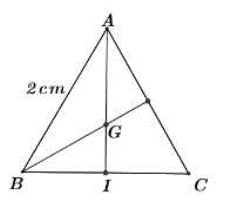
Tam giác đều thì tâm đường tròn ngoại tiếp tam giác trùng với trọng tâm, từ đó áp dụng định lý Pytago.
Cách giải
Gọi I là trung điểm của BC, G là trọng tâm tam giác ABC và R là bán kính đường tròn ngoại tiếp tam giác ABC thì .
Trong tam giác ABI vuông tại I có:
Khi đó: .
Hot: 500+ Đề thi vào 10 file word các Sở Hà Nội, TP Hồ Chí Minh có đáp án 2025 (chỉ từ 100k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đáp án B
Phương pháp
Thay tọa độ điểm A vào lần lượt các đáp án.
Cách giải
Thay tọa độ điểm vào phương trình các đường thẳng ta được:
+ Ý A: (loại).
+ Ý B: (đúng) chọn đáp án B.
Lời giải
Đáp án C
Phương pháp
Áp dụng định lý Pytago trong tam giác vuông.
Cách giải
Gọi cạnh góc vuông nhỏ của tam giác vuông bài cho là .
Khi đó cạnh góc vuông còn lại là: 2a.
Áp dụng định lý Pytago ta có cạnh huyền là: .
Cạnh huyền gấp lần cạnh góc vuông nhỏ nhất của tam giác đó.
Câu 3
A. Tiếp xúc ngoài.
B. Đựng nhau.
C. Tiếp xúc trong.
D. Cắt nhau.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. .
B. .
C. .
D. .
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo