1) Giải hệ phương trình sau 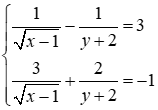
2) Cho Parabol 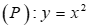 và đường thẳng (d): y = 2x + 3
và đường thẳng (d): y = 2x + 3
a) Chứng minh rằng đường thẳng d cắt parabol (P) tại hai điểm phân biệt A, B và tìm tọa độ của A, B
b) Xác định điểm C thuộc cung nhỏ AB của parabol (P) sao cho diện tích 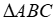 lớn nhất .
lớn nhất .
1) Giải hệ phương trình sau 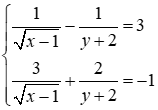
2) Cho Parabol ![]() và đường thẳng (d): y = 2x + 3
và đường thẳng (d): y = 2x + 3
a) Chứng minh rằng đường thẳng d cắt parabol (P) tại hai điểm phân biệt A, B và tìm tọa độ của A, B
b) Xác định điểm C thuộc cung nhỏ AB của parabol (P) sao cho diện tích ![]() lớn nhất .
lớn nhất .
Câu hỏi trong đề: Đề kiểm tra giữa học kì 2 môn Toán 9 có đáp án (Mới nhất) !!
Quảng cáo
Trả lời:
\(1)\left\{ \begin{array}{l}\frac{1}{{\sqrt {x - 1} }} - \frac{1}{{y + 2}} = 3\\\frac{3}{{\sqrt {x - 1} }} + \frac{2}{{y + 2}} = - 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\sqrt {x - 1} = 1\\y + 2 = - \frac{1}{2}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 2\\y = - \frac{5}{2}\end{array} \right.\)
\({x^2} - 2x - 3 = 0 \Leftrightarrow \left[ \begin{array}{l}{x_A} = 3 \Rightarrow A\left( {3;9} \right)\\{x_B} = - 1 \Rightarrow B\left( { - 1;1} \right)\end{array} \right.\)
b) \(C\left( {x;{x^2}} \right)\)và \(A',B',C'\)lần lượt là chân đường cao hạ xuống \(Ox\)
\(\begin{array}{l}{S_{ABC}} = {S_{AA'B'B}} + {S_{ACC'A'}} - {S_{BCC'B'}} = 2{x^2} + 4x + 6 = 8 - 2{\left( {x - 1} \right)^2} \le 8\\ \Rightarrow MaxS = 8 \Leftrightarrow C\left( {1;1} \right)\end{array}\)
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Gọi \(x\)là số công nhân, \(y\)là số ngày dự định \(\left( {x,y \in N*,x > 10} \right)\)
Theo bài ta có hệ phương trình :
\(\left\{ \begin{array}{l}\left( {x + 10} \right)\left( {y - 2} \right) = xy\\\left( {x - 10} \right)\left( {y + 3} \right) = xy\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} - 2x + 10y = 20\\3x - 10y = 30\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 50\\y = 12\end{array} \right.(tm)\)
Vậy có 50 công nhân, làm trong 12 ngày
Lời giải
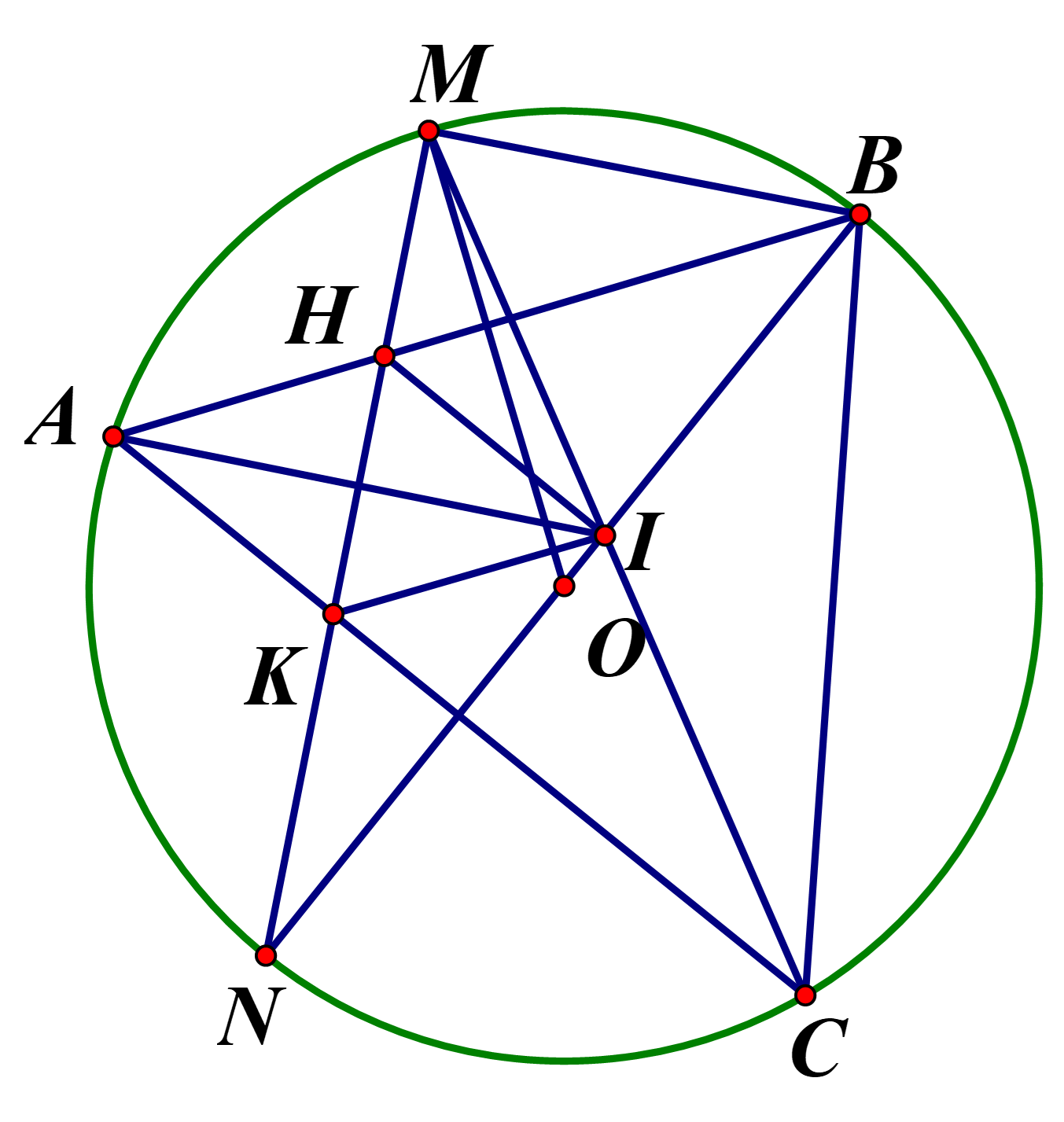
\( \Rightarrow \angle HMB + \angle HIB = 180^\circ \)mà \(\angle NIH + \angle HIB = 180^\circ \Rightarrow \angle HNB = \angle HIB\)
Xét \(\Delta NIH\)và \(\Delta NMB\)có: \(\angle MNB\)chung,
\( \Rightarrow \frac{{NI}}{{NM}} = \frac{{NH}}{{NB}} \Rightarrow NI.NB = NM.NH\)
\( \Rightarrow \angle KIN = \angle KCN\)(cùng chắn mà \(\angle KCN = \angle ABN\)(cùng chắn
\( \Rightarrow \angle KIN = \angle ABN\), mà chúng đồng vi \( \Rightarrow KI//AH\left( 1 \right)\)
Theo câu 1, tứ giác \(BHMI\)nội tiếp \( \Rightarrow \angle IMB = \angle IHB\)(cùng chắn
Mà \(\angle IMB = \angle CAB\), mà chúng đồng vị \( \Rightarrow IH//AK\left( 2 \right)\)
Từ (1) và (2) \( \Rightarrow AHIK\)là hình bình hành
Lại có :
\( \Rightarrow \angle AKH = \angle AHK \Rightarrow \Delta AHK\)cân tại A\( \Rightarrow AH = AK\)
Hình bình hành \(AHIK\)có \(AN = AK \Rightarrow AHIK\)là hình thoi\( \Rightarrow KH\)là đường phân giác \(\angle AKI \Rightarrow IA\)là phân giác \(\angle KIH\)
\( \Rightarrow \Delta {O_1}AH\)cân tại \({O_1}\)và \(\Delta {O_2}BH\)cân tại \({O_2}\), có \(\angle A{O_1}H = 2\angle ANH\), \(\angle B{O_2}H = 2\angle BNH\)\( \Rightarrow \angle {A_1}OH = \angle B{O_2}H\)mà \(\angle ANH = \angle BNH\)
\( \Rightarrow \angle {O_1}AH = \angle {O_1}HA = \angle {O_2}HB = \angle O_2^{}BH\)
Gọi D là giao điểm của \(A{O_1}\)và \(B{O_2}\)có:
\(\Delta ADB\)cân tại \(D \Rightarrow M,O,D\)thẳng hàng
Có \(\angle AMD = \angle MAB = \angle ANM \Rightarrow MA\)là tiếp tuyến của \(\left( {{O_1}} \right) \Rightarrow \angle MAD = 90^\circ \)\( \Rightarrow MD\)là đường kính của \(\left( O \right) \Rightarrow D\)cố định
Ta chứng minh được : \(\angle A{O_1}H = \angle ADB \Rightarrow H{O_1}//D{O_2}\)
\( \Rightarrow \angle AOB = \angle H{O_2}B \Rightarrow H{O_2}//D{O_1}\)
Tứ giác \(H{O_1}D{O_2}\)là hình bình hành\( \Rightarrow {O_2}H = D{O_1}\)
Có \({R_1} + {R_2} = {O_1}A + {O_2}H = {O_1}A + {O_1}D = AD\)
\(A,D\)cố định \( \Rightarrow AD\)không đổi \( \Rightarrow {R_1} + {R_2}\)không đổi
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
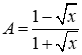
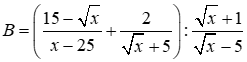 với
với