Một xe khách và một xe du lịch khởi hành cùng một lúc từ A đến B. Xe du lịch có vận tốc lớn hơn vận tốc của xe khách là 20km/h, do đó nó đến B trước xe khách 25 phút. Tính vận tốc mỗi xe, biết khoảng cách AB là 100km.
Câu hỏi trong đề: Đề kiểm tra giữa học kì 2 môn Toán 9 có đáp án (Mới nhất) !!
Quảng cáo
Trả lời:
Gọi \(x\)là vận tốc xe khách, \(y\)là vận tốc xe du lịch \(\left( {x > 0,y > 20} \right);25' = \frac{5}{{12}}h\)
Theo bài ta có hệ : \(\left\{ \begin{array}{l}x - y = 20\\\frac{{100}}{y} - \frac{{100}}{x} = \frac{5}{{12}}\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}y = 60(tm) \Rightarrow x = 80(tm)\\y = - 80(ktm)\end{array} \right.\)
Vậy vận tốc xe du lịch: 80km/h, vận tốc xe khách: \(60km/h\)
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
\(2{x^2} - \left( {4m + 3} \right)x + 2{m^2} - 1 = 0 & (1)\)
\(\Delta = {\left( {4m + 3} \right)^2} - 4.2\left( {2{m^2} - 1} \right) = 24m + 17\)
Để \(\left( 1 \right)\)có nghiệm thì \(\Delta \ge 0 \Leftrightarrow 24m + 17 \ge 0 \Leftrightarrow m \ge \frac{{ - 17}}{{24}}\)
Lời giải
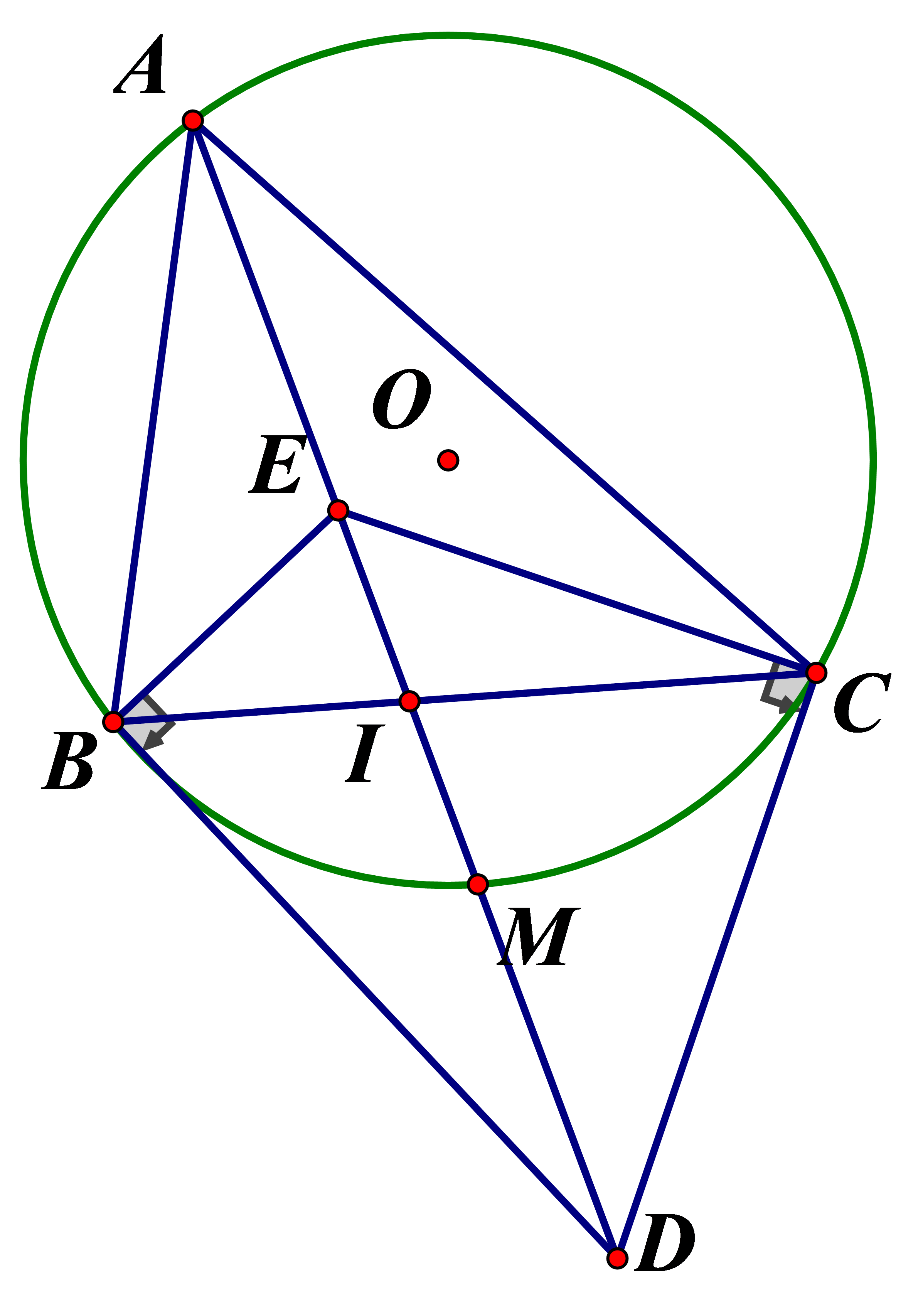
a) Vì \(E\)là giao điểm của hai phân giác \(\angle B\)và \(\angle C\)của tam giác \(ABC\)nên \(AE\)cũng là phân giác của \(\angle A\). Khi đó \(AE,AD\)đều là phân giác trong \(\angle BAC\)nên
\(A,E,D\)thẳng hàng
b) Ta có : \(\angle EBD + \angle ECD = 90^\circ + 90^\circ = 180^\circ \Rightarrow BECD\)là tứ giác nội tiếp
c) Xét \(\Delta BIE\)và \(\Delta DIC\)có : \(\angle EBC = \angle EDC\)(cùng chắn ; \(\angle BIE = \angle DIC\)(đối đỉnh) \( \Rightarrow \frac{{BI}}{{ID}} = \frac{{IE}}{{IC}} \Rightarrow BI.IC = ID.IE\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.