Một con lắc lò xo có độ cứng k = 40 N/m gắn với quả cầu có khối lượng m. Cho quả cầu dao động với biên độ 5 cm. Hãy tính động năng của quả cầu khi nó ở vị trí có li độ x = 3 cm.
Một con lắc lò xo có độ cứng k = 40 N/m gắn với quả cầu có khối lượng m. Cho quả cầu dao động với biên độ 5 cm. Hãy tính động năng của quả cầu khi nó ở vị trí có li độ x = 3 cm.
A. 0,032 J
B. 320 mJ
C. 0,018 J
D. 0,5 J
Câu hỏi trong đề: (2023) Đề thi thử Vật Lí THPT Trần Cao Vân có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Hot: 1000+ Đề thi giữa kì 1 file word cấu trúc mới 2025 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
- Sổ tay Vật lí 12 (chương trình mới) ( 18.000₫ )
- 1000 câu hỏi lí thuyết môn Vật lí (Form 2025) ( 45.000₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
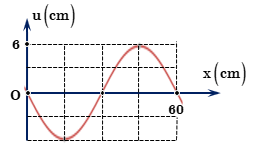
Gọi A là biên độ bụng, ta có : \[\begin{array}{l}\omega \sqrt {{A^2} - {u^2}} = \frac{{15\pi }}{{100}}v \Leftrightarrow \frac{{2\pi }}{T}\sqrt {{A^2} - {u^2}} = \frac{{15\pi }}{{100}}\frac{\lambda }{T}\\ \Rightarrow \sqrt {{A^2} - {u^2}} = \frac{{15\lambda }}{{200}} = \frac{{15.60}}{{200}} = 4,5cm.\end{array}\]
\[ = > A = \sqrt {4,{5^2} + {6^2}} = 7,5cm\]
Câu 2
A. \[\frac{1}{2}m{v^2} + k{x^2}\]
B. \[m{v^2} + k{x^2}\]
C. \[\frac{1}{2}m{v^2} + \frac{1}{2}k{x^2}\]
D. \[\frac{1}{2}mv + \frac{1}{2}kx\]
Lời giải
Cơ năng của con lắc lò xo được xác định bởi biểu thức \(\frac{1}{2}m{v^2} + \frac{1}{2}k{x^2}\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. 2f
B. f
C. 2/f
D. 1/f
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. âm thanh.
B. hạ âm.
C. siêu âm.
D. cao tần.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. \(120\;{\rm{W}};45\;\Omega \).
B. \(60\;{\rm{W}};90\;\Omega \).
C. \(60\;{\rm{W}};80\;\Omega \).
D. \(120\,{\rm{W}};90\,\Omega \).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo