Câu hỏi:
18/04/2023 2,790
Đặt điện áp \({{\rm{u}}_{{\rm{AB}}}} = 60\sqrt 2 {\rm{cos}}\left( {300{\rm{t}} + \pi /3} \right){\rm{V}}\) vào hai đầu đoạn mạch \({\rm{AB}}\) như hình bên, trong đó \({\rm{R}} = 150{\rm{\Omega }}\) và điện dung C của tụ thay đổi được. Khi \({\rm{C}} = {{\rm{C}}_1}\) thì điện tích của bản tụ điện nối vào \({\rm{N}}\) là \({{\rm{q}}_{\rm{N}}} = 5\sqrt 2 {.10^{ - 4}}{\rm{cos}}\left( {300{\rm{t}} + \pi /6} \right){\rm{C}}.\) Trong các biểu thức, \({\rm{t}}\) tính bằng s. Khi \({\rm{C}} = {{\rm{C}}_2}\) thì điện áp hiệu dụng giữa hai đầu điện trở đạt giá trị cực đại, giá trị đó bằng
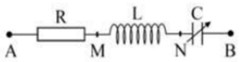
Câu hỏi trong đề: (2023) Đề thi thử Vật Lí Đô Lương 1, Nghệ An có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Hướng dẫn
Khi \(C = {C_1}\) thì \(i = q' = 5\sqrt 2 {.10^{ - 4}}.300.\cos \left( {300t + \frac{\pi }{6} + \frac{\pi }{2}} \right) = 0,15\sqrt 2 \cos \left( {300t + \frac{{2\pi }}{3}} \right)\) (A)
\(\left( {R + r} \right) + \left( {{Z_L} - {Z_C}} \right)j = \frac{u}{i} = \frac{{60\sqrt 2 \angle \frac{\pi }{3}}}{{0,15\sqrt 2 \angle \frac{{2\pi }}{3}}} = 200 - 200\sqrt 3 j \Rightarrow R + r = 200\)
Khi \(C = {C_2}\) thì \({U_{R\max }} = \frac{{UR}}{{R + r}} = \frac{{60.150}}{{200}} = 45\) (V).
Chọn C
Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay
Sách thầy cô Vietjack biên soạn:
- Sổ tay Vật lí 12 (chương trình mới) ( 18.000₫ )
- 20 đề thi tốt nghiệp môn Vật lí (có đáp án chi tiết) ( 38.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Hướng dẫn
\(\tan \left| {{\varphi _{AM}}} \right| = \frac{{{Z_C}}}{R} \Rightarrow \tan \frac{\pi }{4} = \frac{{{Z_C}}}{R} \Rightarrow {Z_C} = R\)
\(\tan \varphi = \frac{{{Z_L} - {Z_C}}}{R} \Rightarrow \tan \frac{\pi }{4} = \frac{{{Z_L} - {Z_C}}}{{{Z_C}}} \Rightarrow \frac{{{Z_C}}}{{{Z_L}}} = 0,5\). Chọn A
Lời giải
Hướng dẫn
\(u = {u_d} + {u_C} = 90\sqrt 2 \angle \frac{\pi }{3} + 90\sqrt 2 \angle \frac{{ - \pi }}{3} = 90\sqrt 2 \angle 0 \Rightarrow {U_2} = 90V\)
\(\frac{{{N_1}}}{{{U_1}}} = \frac{{{N_2}}}{{{U_2}}} = \frac{{{N_1} + {N_2}}}{{{U_1} + {U_2}}} \Rightarrow \frac{{{N_1}}}{{240}} = \frac{{5500}}{{240 + 90}} \Rightarrow {N_1} = 4000\) vòng. Chọn B
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
Đề thi thử tốt nghiệp THPT môn Vật lí Sở Giáo dục và Đào tạo Nam Định có đáp án
-
(2025 mới) Đề ôn thi tốt nghiệp THPT Vật lí (Đề số 1)
-
Đề minh họa tốt nghiệp THPT môn Vật lý có đáp án năm 2025 (Đề 3)
-
Đề minh họa tốt nghiệp THPT môn Vật lý có đáp án năm 2025 (Đề 2)
-
Đề minh họa tốt nghiệp THPT môn Vật lý có đáp án năm 2025 (Đề 4)
-
Đề thi thử tốt nghiệp THPT môn Vật lí THPT Trưng Yên - Hưng Yên có đáp án
-
Đề thi thử tốt nghiệp THPT môn Vật lí THPT Yên Lạc - Vĩnh Phúc - Lần 1 có đáp án
-
(2025 mới) Đề ôn thi tốt nghiệp THPT Vật lí (Đề số 6)
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận