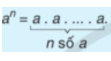Câu hỏi:
03/07/2023 307
Dãy số Fibonacci được định nghĩa đệ quy như sau:
+ Phần cơ sở: F(w) = 0 nếu n = 0. F(n) = 1 nếu n > 1.
+ Phần đệ quy: F(n) = F (n - 1) + F(n - 2) nếu n >2
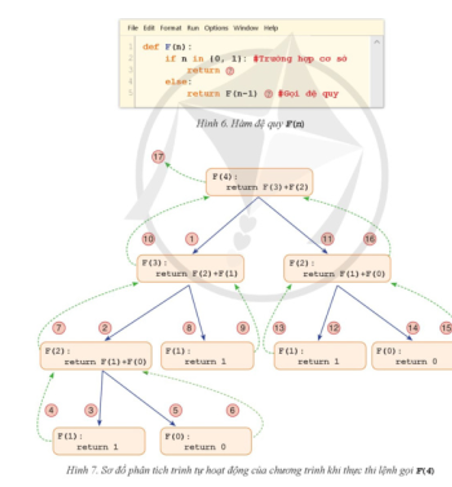
Hàm đệ quy F (n) cho trong hình 6s dụng định nghĩa đệ quy ở trên để tính và trả về giả trị của F(n).
a) Em hãy cho biết các dấu ? trong bàm đệ quy F(n) của được thay bằng gì?
b) Hình 7 liệt kê lần lượt I7 bước chương trình sẽ thực luôn khi lời gọi đến F(4) được thực thi. Em hãy đưa ra giải thích bằng lới ý nghĩa của I7 bước đã cho.
Dãy số Fibonacci được định nghĩa đệ quy như sau:
+ Phần cơ sở: F(w) = 0 nếu n = 0. F(n) = 1 nếu n > 1.
+ Phần đệ quy: F(n) = F (n - 1) + F(n - 2) nếu n >2
Hàm đệ quy F (n) cho trong hình 6s dụng định nghĩa đệ quy ở trên để tính và trả về giả trị của F(n).
a) Em hãy cho biết các dấu ? trong bàm đệ quy F(n) của được thay bằng gì?
b) Hình 7 liệt kê lần lượt I7 bước chương trình sẽ thực luôn khi lời gọi đến F(4) được thực thi. Em hãy đưa ra giải thích bằng lới ý nghĩa của I7 bước đã cho.
Quảng cáo
Trả lời:
Giải bởi Vietjack
a) return 1
else
return F (n - 1)
b) Ý nghĩa của I7 bước đã cho.
Trong hàm có một hoặc nhiều lệnh gọi đến chính nó.
Mỗi lần gọi đệ quy thì kích thước của bài toán được thu nhỏ hơn so với lần gọi trước. Khi đạt được trường hợp cơ sở thì chương trình không cần gọi đệ quy.
Thuật toán đệ quy được cài đặt dưới dạng hàm đệ quy, để xử lí với các đối tượng được định nghĩa đệ quy.
Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay
Sách thầy cô Vietjack biên soạn:
- Trọng tâm Sử, Địa, GD KTPL 11 cho cả 3 bộ Kết nối, Chân trời, Cánh diều VietJack - Sách 2025 ( 38.000₫ )
- Trọng tâm Hóa học 11 dùng cho cả 3 bộ sách Kết nối, Cánh diều, Chân trời sáng tạo VietJack - Sách 2025 ( 58.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
a) return 1
else
return F (n - 1)
b) Ý nghĩa của I7 bước đã cho.
Trong hàm có một hoặc nhiều lệnh gọi đến chính nó.
Mỗi lần gọi đệ quy thì kích thước của bài toán được thu nhỏ hơn so với lần gọi trước. Khi đạt được trường hợp cơ sở thì chương trình không cần gọi đệ quy.
Thuật toán đệ quy được cài đặt dưới dạng hàm đệ quy, để xử lí với các đối tượng được định nghĩa đệ quy.
Lời giải
Những câu sau đây đúng khi nói về hàm đệ quy:
c) Hàm đệ quy là hàm mà thân hàm có chứa những lệnh gọi đến chính nó.
đ) Hàm đệ quy được sử dụng để cài đặt thuật toán đệ quy.
g) Hàm đệ quy không bao giờ dừng nếu không có trường hợp cơ sở.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
Bộ 4 đề thi cuối học kì 2 Tin 11 Kết nối tri thức có đáp án (Đề 2)
-
15 câu Trắc nghiệm Tin học 11 Kết nối tri thức Bài 26 có đáp án
-
Bộ 4 đề thi cuối học kì 2 Tin 11 Kết nối tri thức có đáp án (Đề 1)
-
15 câu Trắc nghiệm Tin học 11 Cánh diều Bài 1: Một số thao tác chỉnh sửa ảnh và hỗ trợ chỉnh sửa ảnh có đáp án
-
15 câu Trắc nghiệm Tin học 11 Kết nối tri thức Bài 25 có đáp án
-
15 câu Trắc nghiệm Tin học 11 Kết nối tri thức Bài 28 có đáp án
-
15 câu Trắc nghiệm Tin học 11 Kết nối tri thức Bài 27 có đáp án
-
15 câu Trắc nghiệm Tin học 11 Cánh diều Bài 2: Tẩy xóa ảnh có đáp án
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận