Câu hỏi:
16/04/2024 250
Cho hình lăng trụ tam giác \(ABC.A'B'C'\). Gọi \(M,\,N\) lần lượt là trung điểm của \(A'B'\) và \(AB\).
a) Chứng minh \(CB'\,\,{\rm{//}}\,\left( {AMC'} \right)\).
b) Mặt phẳng \(\left( P \right)\) đi qua \(N\) song song với hai cạnh \(AB'\) và \(AC'\). Tìm giao tuyến của hai mặt phẳng \(\left( P \right)\) và \(\left( {BB'C'} \right)\).
Cho hình lăng trụ tam giác \(ABC.A'B'C'\). Gọi \(M,\,N\) lần lượt là trung điểm của \(A'B'\) và \(AB\).
a) Chứng minh \(CB'\,\,{\rm{//}}\,\left( {AMC'} \right)\).
b) Mặt phẳng \(\left( P \right)\) đi qua \(N\) song song với hai cạnh \(AB'\) và \(AC'\). Tìm giao tuyến của hai mặt phẳng \(\left( P \right)\) và \(\left( {BB'C'} \right)\).
Câu hỏi trong đề: Đề kiểm tra Cuối kì 1 Toán 11 Cánh Diều có đáp án !!
Bắt đầu thiQuảng cáo
Trả lời:
Giải bởi Vietjack
a)
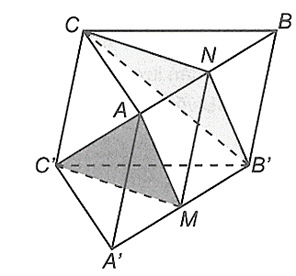
Vì \(M,\,N\) lần lượt là trung điểm của \(A'B'\) và \(AB\) nên \(MN\) là đường trung bình của hình thang \(ABB'A'\). Suy ra \(MN{\rm{//}}AA'\) và \(MN\, = \,AA'\) (do \(ABB'A'\) là hình bình hành).
Ta có: \[MN{\rm{//}}AA'\] và \[AA'{\rm{//}}CC'\] (tính chất hình lăng trụ).
\[ \Rightarrow MN{\rm{//AA'}}{\rm{.}}\]
Lại có \(AA' = CC'\) (tính chất hình lăng trụ), mà \(MN\, = \,AA'\) nên \[MN = CC'\].
Do đó, tứ giác \[MNCC'\] là hình bình hành. Suy ra \[CN{\rm{//}}MC'.\]
Ta có \[\left\{ \begin{array}{l}CN{\rm{ // }}MC'\\MC' \subset \left( {AMC'} \right)\end{array} \right. \Rightarrow CN{\rm{ // }}\left( {AMC'} \right).\]
Mặt khác ta chứng minh được \[AN{\rm{//}}B'M;\,\,AN = B'M\] nên tứ giác \[ANB'M\] là hình bình hành. Suy ra \[NB'{\rm{//}}MA.\]
Ta có \[\left\{ \begin{array}{l}NB'{\rm{//}}MA\\MA \subset \left( {AMC'} \right)\end{array} \right. \Rightarrow NB'{\rm{//}}\left( {AMC'} \right).\]
Lại có \[\left\{ \begin{array}{l}CN{\rm{//}}\left( {AMC'} \right)\\NB'{\rm{//}}\left( {AMC'} \right)\\CN,NB' \subset \left( {CNB'} \right)\\CN \cap NB' = \left\{ N \right\}\end{array} \right. \Rightarrow \left( {AMC'} \right){\rm{//}}\left( {CNB'} \right).\]
Mà \[CB' \subset \left( {CNB'} \right).\,\,\,{\rm{Suy}}\,\,{\rm{ra}}\,\,\,CB'\,{\rm{//}}\,\left( {AMC'} \right)\].
b)
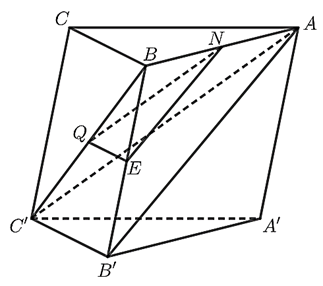
Trong mặt phẳng \(\left( {ABB'A'} \right)\), kẻ đường thẳng qua \(N\) song song với \(AB'\), cắt \(BB'\) tại \(E\).
Trong mặt phẳng \(\left( {ABC'} \right)\), kẻ đường thẳng qua \(N\) song song với \(AC'\), cắt \(BC'\) tại \(Q\).
Khi đó, mặt phẳng \(\left( P \right)\) chính là mặt phẳng \(\left( {NQE} \right)\).
Vì \(E \in BB'\) nên \(E \in \left( {BB'C'} \right)\); vì \(Q \in BC'\) nên \(Q \in \left( {BB'C'} \right)\). Do đó, \(EQ \subset \left( {BB'C'} \right)\).
Vậy \[\left( {NQE} \right) \cap \left( {BB'C'} \right)\,\, = \,\,EQ\] hay \[\left( P \right) \cap \left( {BB'C'} \right)\,\, = \,\,EQ\].
Nhà sách vietjack
Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay
- Sách - Sổ tay kiến thức trọng tâm Vật lí 11 VietJack - Sách 2025 theo chương trình mới cho 2k8 ( 45.000₫ )
- Trọng tâm Sử, Địa, GD KTPL 11 cho cả 3 bộ Kết nối, Chân trời, Cánh diều VietJack - Sách 2025 ( 38.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 2:
Cho hình lăng trụ \[ABC.{A_1}{B_1}{C_1}.\] Trong các khẳng định sau, khẳng định nào sai?
Cho hình lăng trụ \[ABC.{A_1}{B_1}{C_1}.\] Trong các khẳng định sau, khẳng định nào sai?
Xem đáp án »
16/04/2024
2,015
Câu 3:
Tập xác định của hàm số \[y = \tan \left( {x + \frac{\pi }{3}} \right)\] là
Tập xác định của hàm số \[y = \tan \left( {x + \frac{\pi }{3}} \right)\] là
Xem đáp án »
16/04/2024
1,771
Câu 4:
Cho tứ diện \(ABCD,\) vị trí tương đối của hai đường thẳng \(AC\) và \(BD\) là
Cho tứ diện \(ABCD,\) vị trí tương đối của hai đường thẳng \(AC\) và \(BD\) là
Xem đáp án »
16/04/2024
1,699
Câu 5:
Kết quả của giới hạn \(\mathop {\lim }\limits_{x \to - 1} \left( {x + 1} \right)\) là
Kết quả của giới hạn \(\mathop {\lim }\limits_{x \to - 1} \left( {x + 1} \right)\) là
Xem đáp án »
16/04/2024
1,270
Câu 7:
Cho hình vuông \(\left( {{C_1}} \right)\) có cạnh bằng \(a.\) Người ta chia mỗi cạnh của hình vuông thành bốn phần bằng nhau và nối các điểm chia một cách thích hợp để có hình vuông \(\left( {{C_2}} \right)\) (xem hình vẽ). Từ hình vuông \(\left( {{C_2}} \right)\) lại tiếp tục làm như trên ta nhận được dãy các hình vuông \({C_1},\,\,{C_2},\,\,{C_3},\,...,\,{C_n},\,...\). Gọi \({S_i}\) là diện tích của hình vuông \({C_i}\,\,\left( {i \in \left\{ {1;\,\,2;\,\,3;\,\,...} \right\}} \right)\). Đặt \(T = {S_1} + {S_2} + {S_3} + ... + {S_n} + ...\). Biết \(T = \frac{{32}}{3}\), tính \(a.\)
Xem đáp án »
16/04/2024
950
🔥 Đề thi HOT:
-
10 Bài tập Nhận biết góc phẳng của góc nhị diện và tính góc phẳng nhị diện (có lời giải)
-
Bài tập Hình học không gian lớp 11 cơ bản, nâng cao có lời giải (P11)
-
10 Bài tập Biến cố hợp. Biến cố giao (có lời giải)
-
100 câu trắc nghiệm Đạo hàm cơ bản (P1)
-
38 câu trắc nghiệm Toán 11 Kết nối tri thức Lôgarit có đáp án
-
10 Bài tập Nhận biết góc phẳng của góc nhị diện và tính góc phẳng nhị diện (có lời giải)
-
15 câu Trắc nghiệm Khoảng cách có đáp án (Nhận biết)
-
Bài tập Xác suất ôn thi THPT Quốc gia có lời giải (P1)
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận