Trong một trò chơi, các câu hỏi gồm hai loại I và II.
+) Với câu hỏi loại I: Trả lời đúng được 20 điểm. Trả lời sai không được điểm (0 điểm).
+) Với câu hỏi loại II. Trả lời đúng được 80 điểm. Trả lời sai không được điểm (0 điểm).
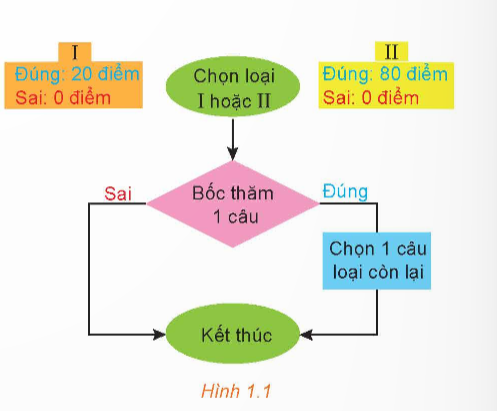
Ở vòng 1, người chơi được chọn một trong hai loại câu hỏi. Sau khi chọn xong loại câu hỏi, người chơi bốc thăm ngẫu nhiên một câu hỏi trong loại đó. Nếu trả lời sai thì phải dừng cuộc chơi. Nếu trả lời đúng, thí sinh sẽ bước vào vòng 2, bốc ngẫu nhiên một câu hỏi trong loại còn lại. Người chơi trả lời đúng hay sai, cuộc chơi cũng kết thúc tại đây. Giả thiết rằng việc trả lời đúng câu hỏi vòng 1 sẽ không ảnh hưởng đến xác suất trả lời đúng hay sai câu hỏi ở vòng 2.
Bạn Minh tham gia cuộc chơi. Giả sử xác suất để Minh trả lời đúng câu hỏi loại I là 0,8; xác suất để Minh trả lời đúng câu hỏi loại II là 0,6. Hỏi ở vòng 1 Minh nên chọn câu hỏi loại I hay câu hỏi loại II?
Trong một trò chơi, các câu hỏi gồm hai loại I và II.
+) Với câu hỏi loại I: Trả lời đúng được 20 điểm. Trả lời sai không được điểm (0 điểm).
+) Với câu hỏi loại II. Trả lời đúng được 80 điểm. Trả lời sai không được điểm (0 điểm).
Ở vòng 1, người chơi được chọn một trong hai loại câu hỏi. Sau khi chọn xong loại câu hỏi, người chơi bốc thăm ngẫu nhiên một câu hỏi trong loại đó. Nếu trả lời sai thì phải dừng cuộc chơi. Nếu trả lời đúng, thí sinh sẽ bước vào vòng 2, bốc ngẫu nhiên một câu hỏi trong loại còn lại. Người chơi trả lời đúng hay sai, cuộc chơi cũng kết thúc tại đây. Giả thiết rằng việc trả lời đúng câu hỏi vòng 1 sẽ không ảnh hưởng đến xác suất trả lời đúng hay sai câu hỏi ở vòng 2.
Bạn Minh tham gia cuộc chơi. Giả sử xác suất để Minh trả lời đúng câu hỏi loại I là 0,8; xác suất để Minh trả lời đúng câu hỏi loại II là 0,6. Hỏi ở vòng 1 Minh nên chọn câu hỏi loại I hay câu hỏi loại II?

Quảng cáo
Trả lời:
Sau khi học xong bài này, ta giải quyết được bài toán này như sau:
+) Giả sử ở vòng 1 bạn Minh chọn câu hỏi loại I
Gọi X là số điểm Minh nhận được.
Số điểm trung bình mà Minh nhận được là E(X).
Gọi A là biến cố: “Minh trả lời đúng câu hỏi loại I”; B là biến cố: “Minh trả lời đúng câu hỏi loại II”.
Theo đề ta có P(A) = 0,8; P(B) = 0,6.
Vòng 1: Minh bốc ngẫu nhiên một câu hỏi loại I. Có hai khả năng
- Nếu trả lời sai thì Minh nhận 0 điểm. Cuộc chơi kết thúc tại đây.
Ta có {X = 0} = ![]() . Do đó P(X = 0) =
. Do đó P(X = 0) = ![]() .
.
- Nếu trả lời đúng thì Minh nhận 20 điểm và Minh sẽ bước vào vòng 2.
Vòng 2: Minh bốc ngẫu nhiên một câu hỏi loại II. Khi đó có hai khả năng:
- Nếu trả lời sai, Minh không có điểm và phải dừng cuộc chơi với tổng số điểm nhận được là 20 + 0 = 20 điểm.
Ta có {X = 20} = ![]() . Theo giả thiết A và B là hai biến cố độc lập nên A và
. Theo giả thiết A và B là hai biến cố độc lập nên A và ![]() cũng độc lập.
cũng độc lập.
Theo công thức nhân xác suất cho hai biến cố độc lập ta có:
P(X = 20) = ![]() .
.
- Nếu trả lời đúng Minh nhận 80 điểm. Cuộc thi kết thúc tại đây và tổng số điểm Minh nhận được là: 20 + 80 = 100 điểm.
Ta có {X = 100} = AB. Theo giả thiết A và B là hai biến cố độc lập.
Theo công thức nhân xác suất cho hai biến cố độc lập ta có:
P(X = 100) = P(AB) = P(A).P(B) = 0,8.0,6 = 0,48.
Bảng phân bố xác suất của X

Từ đó E(X) = 0.0,2 + 20.0,32 + 100.0,48 = 54,4.
Vậy nếu chọn câu hỏi loại I ở vòng 1 thì trung bình Minh được 54,4 điểm.
+) Giả sử ở vòng 1 bạn Minh chọn câu hỏi loại II
Gọi Y là số điểm Minh nhận được. Ta lập bảng phân bố xác suất của Y.
Gọi A là biến cố “Minh trả lời đúng câu hỏi loại I”; B là biến cố “Minh trả lời đúng câu hỏi loại II”.
Theo đề có P(A) = 0,8; P(B) = 0,6.
+) Nếu trả lời sai: Minh được 0 điểm. Cuộc chơi kết thúc tại đây.
Vậy P(Y = 0) = ![]() .
.
+) Nếu trả lời đúng Minh nhận 80 điểm và Minh sẽ bước vào vòng 2, bốc ngẫu nhiên một câu hỏi loại I.
Nếu trả lời sai, Minh không có điểm và phải dừng cuộc chơi với số điểm nhận được là 80 + 0 = 80 điểm. Theo giả thiết A và B là hai biến cố độc lập. Theo công thức nhân xác suất cho hai biến cố độc lập ta có:
P(Y = 80) = ![]() .
.
Nếu trả lời đúng Minh nhận 20 điểm. Cuộc chơi kết thúc tại đây và Minh được 20 + 80 = 100 điểm. Theo công thức nhân xác suất cho hai biến cố độc lập ta có:
P(Y = 100) = P(BA) = P(B).P(A) = 0,6.0,8 = 0,48.
Bảng phân bố xác suất của Y là

Ta có E(Y) = 0.0,4 + 80.0,12 + 100.0,48 = 57,6.
Vậy trung bình Minh được 57,6 điểm.
Ta có E(X) = 54,4. Vì E(Y) > E(X) nên nếu ở vòng I Minh chọn câu hỏi loại II thì về trung bình Minh được nhiều điểm hơn. Vậy ở vòng 1, Minh nên chọn câu hỏi loại II.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Các giá trị của X thuộc tập {0; 1; 2; 3}.
Ta cần tính P(X = 0), P(X = 1), P(X = 2), P(X = 3).
Số kết quả có thể là ![]() .
.
+) Biến cố (X = 0) là biến cố: “Chọn được 3 học sinh nữ”.
Số kết quả thuận lợi cho biến cố (X = 0) là ![]() .
.
Vậy 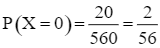 .
.
+) Biến cố (X = 1) là biến cố: “Chọn được 1 học sinh nam và 2 học sinh nữ”.
Có ![]() cách chọn 1 học sinh nam trong 10 học sinh nam và
cách chọn 1 học sinh nam trong 10 học sinh nam và ![]() cách chọn 2 học sinh nữ trong 6 học sinh nữ.
cách chọn 2 học sinh nữ trong 6 học sinh nữ.
Theo quy tắc nhân ta có 10.15 = 150 cách chọn 1 học sinh nam và 2 học sinh nữ.
Vậy số kết quả thuận lợi cho biến cố (X = 1) là 150.
Do đó P(X = 1) = 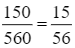 .
.
+) Biến cố (X = 2) là biến cố: “Chọn được 2 học sinh nam và 1 học sinh nữ”.
Có ![]() cách chọn 2 học sinh nam trong 10 học sinh nam và
cách chọn 2 học sinh nam trong 10 học sinh nam và ![]() cách chọn 1 học sinh nữ trong 6 học sinh nữ. Theo quy tắc nhân ta có 45.6 = 270 cách chọn 2 học sinh nam và 1 học sinh nữ.
cách chọn 1 học sinh nữ trong 6 học sinh nữ. Theo quy tắc nhân ta có 45.6 = 270 cách chọn 2 học sinh nam và 1 học sinh nữ.
Vậy số kết quả thuận lợi cho biến cố (X = 2) là 270.
Do đó 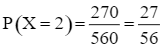 .
.
+) Biến cố (X = 3) là biến cố: “Chọn được 3 học sinh nam”.
Số kết quả thuận lợi cho biến cố (X = 3) là ![]() .
.
Do đó 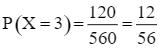 .
.
Vậy bảng phân bố xác suất của X là:
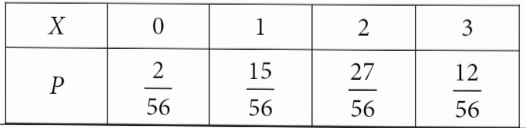
Lời giải
Kí hiệu Aij là biến cố: “Chọn được quả cầu ghi số i và quả cầu ghi số j”.
Giá trị của X thuộc tập {2; 3; 4; 5; 6; 7}.
Ta có P(X = 2) = P(A11) = 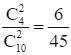 .
.
P(X = 3) = P(A12) = 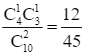 .
.
P(X = 4) = P(A13) + P(A22) = 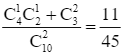 .
.
P(X = 5) = P(A14) + P(A23) = 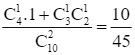 .
.
P(X = 6) = P(A24) + P(A33) = 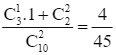 .
.
P(X = 7) = P(A34) = 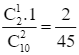
Bảng phân bố xác suất của X là

Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

