Ông Đạt đem gửi hai khoản tiền vào hai ngân hàng khác nhau. Khoản tiền thứ nhất gửi vào ngân hàng A trong 15 tháng, lãi suất 14%/năm. Khoản tiền thứ hai gửi vào ngân hàng B trong 12 tháng với lãi suất 12,5%/năm. Cho biết hai khoản tiền trên chênh lệch nhau 30 triệu đồng, lãi của khoản tiền thứ nhất gấp đôi lãi của khoản tiền thứ hai và cả hai khoản tiền đều tính lãi theo phương thức lãi đơn. Hãy tính khoản tiền ông Đạt gửi ở mỗi ngân hàng.
Ông Đạt đem gửi hai khoản tiền vào hai ngân hàng khác nhau. Khoản tiền thứ nhất gửi vào ngân hàng A trong 15 tháng, lãi suất 14%/năm. Khoản tiền thứ hai gửi vào ngân hàng B trong 12 tháng với lãi suất 12,5%/năm. Cho biết hai khoản tiền trên chênh lệch nhau 30 triệu đồng, lãi của khoản tiền thứ nhất gấp đôi lãi của khoản tiền thứ hai và cả hai khoản tiền đều tính lãi theo phương thức lãi đơn. Hãy tính khoản tiền ông Đạt gửi ở mỗi ngân hàng.
Quảng cáo
Trả lời:
Gọi x và y lần lượt là khoản tiền ông Đạt gửi ở ngân hàng A và B (triệu đồng) (x > 0, y > 0).
Số tiền lãi ông Đạt nhận được từ ngân hàng A sau 15 tháng là:
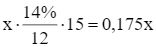 (triệu đồng).
(triệu đồng).
Số tiền lãi ông Đạt nhận được từ ngân hàng B sau 12 tháng là:
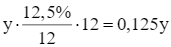 (triệu đồng).
(triệu đồng).
Theo bài, 0,175x = 2 . 0,125y, do đó 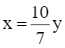 (*) nên x > y.
(*) nên x > y.
Mà hai khoản tiền trên chênh lệch nhau 30 triệu đồng nên ta có x = y + 30, thay vào (*) ta được:
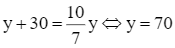 (thỏa mãn).
(thỏa mãn).
Suy ra x = 70 + 30 = 100 (thỏa mãn).
Vậy khoản tiền ông Đạt gửi ở ngân hàng A và B lần lượt là 100 triệu đồng và 70 triệu đồng.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đáp án đúng là: B
Lãi suất danh nghĩa là R = 12%, tỉ lệ lạm phát là i = 4%.
Lãi suất thực là: 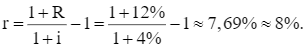
Thực tế, ta có lãi suất thực có thể tính như sau: r’ = R – r = 12% – 4% = 8%.
Lời giải
Do bạn đã không trả đủ toàn bộ số dư nợ và khoản thanh toán tối thiểu tại thời điểm ngày 27/10 nên số tiền lãi sẽ bị tính gồm có:
⦁ Số dư nợ 1 từ ngày 18/9 đến ngày 08/10 nên số tiền lãi phải trả là:
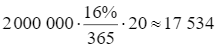 (đồng).
(đồng).
⦁ Số dư nợ 2 từ ngày 08/10 đến ngày 01/11 nên số tiền lãi phải trả là:
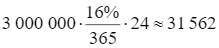 (đồng).
(đồng).
⦁ Tính phí trả chậm:
(4% . 3 000 000) . 2% = 2 400 < 200 000.
Nên tính phí trả chậm là: 200 000 đồng.
Vậy tổng số tiền lãi và phí phát sinh mà bạn cần phải trả đến ngày 01/11 là:
17 534 + 31 562 + 200 000 = 249 096 (đồng).
Ngoài ra, số tiền 2 triệu đồng vẫn bị tính tiếp lãi cho tới thời điểm bạn thanh toán cho ngân hàng.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.