Một phòng học môn Tin học có 40 máy tính được đánh số từ 1 đến 40, các máy cùng loại và cùng màu, mỗi máy được đánh một số khác nhau. Trong phòng học đó, xác suất chọn được một máy tính đã cài đặt phần mềm lập trình Python được đánh số chẵn và được đánh số lẻ lần lượt là 0,375 và 0,45. Bạn Nam chọn ngẫu nhiên một máy tính trong phòng học đó.
Xác suất bạn Nam chọn được máy tính đánh số chẵn, biết rằng máy tính đó đã cài đặt phần mềm lập trình Python, là:
A. 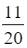 .
.
B. 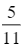 .
.
C. 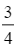 .
.
D. 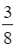 .
.
Xác suất bạn Nam chọn được máy tính đánh số chẵn, biết rằng máy tính đó đã cài đặt phần mềm lập trình Python, là:
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Câu hỏi trong đề: Giải SGK Toán 12 CD Bài 1. Xác suất có điều kiện có đáp án !!
Quảng cáo
Trả lời:
Đáp án đúng là: B
Xét hai biến cố:
C: “Bạn Nam chọn được máy tính được đánh số chẵn”;
A: “Bạn Nam chọn được máy tính đã cài đặt phần mềm lập trình Python”;
Khi đó, xác suất bạn Nam chọn được máy tính đánh số chẵn, biết rằng máy tính đó đã cài đặt phần mềm lập trình Python, chính là xác suất có điều kiện P(C | A).
Vì số máy tính được đánh số lẻ và số máy tính được đánh số chẵn là khác nhau nên hai biến cố A ∩ C và A ∩ B là hai biến cố xung khắc và (A ∩ C) ∪ (A ∩ B) = A, do đó P(A) = P(A ∩ C) + P(A ∩ B) = 0,375 + 0,45 = 0,825.
Khi đó, P(C | A) = 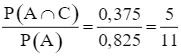 .
.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Xét hai biến cố:
A: “Sản phẩm lấy ra ở lần thứ nhất có chất lượng thấp”;
B: “Sản phẩm lấy ra ở lần thứ hai có chất lượng thấp”.
Khi đó, xác suất để cả hai sản phẩm được lấy ra đều có chất lượng thấp chính là xác suất có điều kiện P(B | A).
Nếu A xảy ra tức là sản phẩm lấy ra ở lần thứ nhất có chất lượng thấp. Khi đó, trong lô sản phẩm còn lại 19 sản phẩm với 4 sản phẩm chất lượng thấp. Vậy P(B | A) = ![]() .
.
Vậy xác suất để cả hai sản phẩm được lấy ra đều có chất lượng thấp là ![]() .
.
Lời giải
Cách 1:
Theo bài ra ta có: n(Ω) = 7 ∙ 7 = 49; n(A) = 3 ∙ 7 = 21; n(B) = 7 ∙ 4 = 28.
Do đó, P(A) = 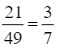 ; P(B) =
; P(B) = 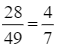 . Suy ra
. Suy ra 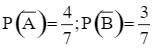 .
.
Ta có biến cố A ∩ B: “Quả bóng màu xanh được lấy ra ở lần thứ nhất và quả bóng màu đỏ được lấy ra ở lần thứ hai”. Suy ra P(A ∩ B) = 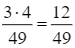 .
.
Khi đó, P(A | B) = 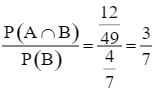 .
.
Ta có biến cố A ∩ ![]() : “Quả bóng màu xanh được lấy ra ở cả hai lần”.
: “Quả bóng màu xanh được lấy ra ở cả hai lần”.
Suy ra P(A ∩ ![]() ) =
) = 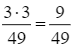 .
.
Khi đó, P(A | ![]() ) =
) = 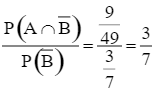 .
.
Vậy ta có P(A) = P(A | B) = P(A | ![]() ) =
) = ![]() . (1)
. (1)
Tương tự, ta tính được:
P(B | A) = 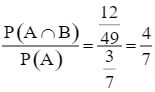 ; P(B |
; P(B | ![]() ) =
) = 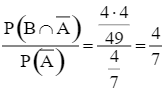 .
.
Vậy ta có P(B) = P(B | A) = P(B | ![]() ) =
) = ![]() . (2)
. (2)
Từ (1) và (2) suy ra A, B là hai biến cố độc lập.
Cách 2:
Nếu A xảy ra, tức là quả bóng màu xanh được lấy ra ở lần thứ nhất. Vì quả bóng lấy ra được bỏ lại vào hộp nên trong hộp có 3 quả bóng xanh và 4 quả bóng đỏ.
Vậy P(B) = ![]() .
.
Nếu A không xảy ra, tức là quả bóng màu đỏ được lấy ra ở lần thứ nhất. Vì quả bóng lấy ra được bỏ lại vào hộp nên trong hộp vẫn có 3 quả bóng xanh và 4 quả bóng đỏ.
Vậy P(B) = ![]() .
.
Như vậy, xác suất xảy ra của biến cố B không thay đổi bởi việc xảy ra hay không xảy ra của biến cố A.
Vì lần thứ nhất lấy và lần thứ hai lấy sau lần thứ nhất nên P(A) = ![]() dù biến cố B có xảy ra hay không xảy ra.
dù biến cố B có xảy ra hay không xảy ra.
Vậy A và B là hai biến cố độc lập.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.