Câu hỏi:
13/07/2024 1,053
Một khinh khí cầu bay với độ cao (so với mực nước biển) tại thời điểm t là h(t), trong đó t tính bằng phút, h(t) tính bằng mét. Tốc độ bay của khinh khí cầu được cho bởi hàm số
v(t) = – 0,12t2 + 1,2t,
với t tính bằng phút, v(t) tính bằng mét/phút. Tại thời điểm xuất phát (t = 0), khinh khí cầu ở độ cao 520 m và 5 phút sau khi xuất phát, khinh khí cầu đã ở độ cao 530 m.
(Nguồn: A. Bigalke et al., Mathematik, Grundkurs ma-1, Cornelsen 2016)
Viết công thức xác định hàm số h(t) (0 ≤ t ≤ 29).
Một khinh khí cầu bay với độ cao (so với mực nước biển) tại thời điểm t là h(t), trong đó t tính bằng phút, h(t) tính bằng mét. Tốc độ bay của khinh khí cầu được cho bởi hàm số
v(t) = – 0,12t2 + 1,2t,
với t tính bằng phút, v(t) tính bằng mét/phút. Tại thời điểm xuất phát (t = 0), khinh khí cầu ở độ cao 520 m và 5 phút sau khi xuất phát, khinh khí cầu đã ở độ cao 530 m.
(Nguồn: A. Bigalke et al., Mathematik, Grundkurs ma-1, Cornelsen 2016)
Viết công thức xác định hàm số h(t) (0 ≤ t ≤ 29).
Câu hỏi trong đề: Giải SGK Toán 12 CD Bài tập cuối Chương 4 có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Hàm số h(t) là một nguyên hàm của hàm số v(t).
Ta có 
.
Suy ra h(t) = – 0,04t3 + 0,6t2 + C.
Vì với t = 0 thì h = 520, tức là h(0) = 520, suy ra C = 520.
Vậy h(t) = – 0,04t3 + 0,6t2 + 520 (0 ≤ t ≤ 29).
Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay
Sách thầy cô Vietjack biên soạn:
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Số ngày công để hoàn thành công trình xây dựng đó là:
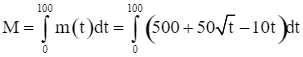
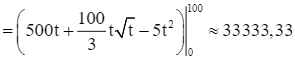(ngày công).
Lời giải
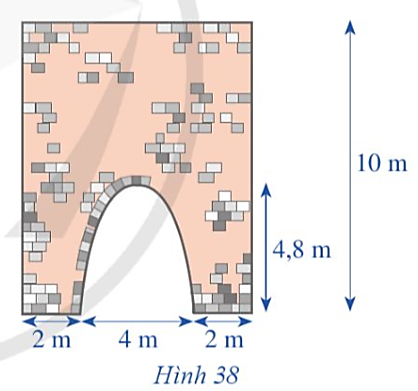
Ta tính diện tích phần cổng hình parabol. Chọn hệ trục tọa độ Oxy với gốc tọa độ O trùng với chân bên trái cổng parabol như hình sau:
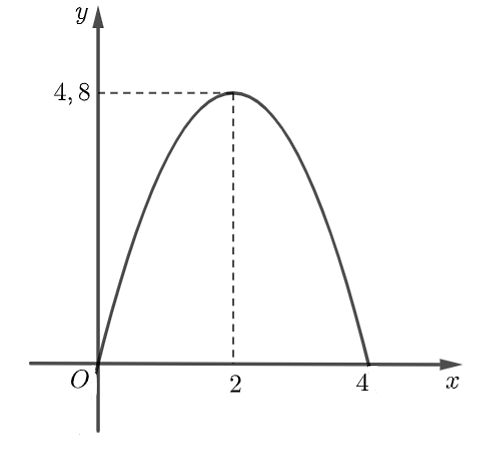
Gọi phương trình parabol là y = f(x) = ax2 + bx + c (a ≠ 0).
Parabol đi qua các điểm (0; 0), (2; 4,8) và (4; 0) nên ta có:
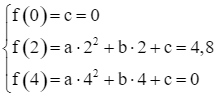. Suy ra 
.
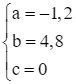Do đó, y = f(x) = – 1,2x2 + 4,8x.
Diện tích phần cổng hình parabol chính là diện tích hình phẳng giới hạn bởi đồ thị hàm số y = f(x) = – 1,2x2 + 4,8x, trục Ox và hai đường thẳng x = 0, x = 4.
Ta có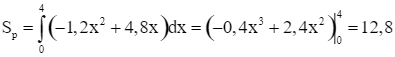 
(m2).
Diện tích phần mặt ngoài của bức tường cần sơn là:
S = 10 ∙ (2 + 4 + 2) – 12,8 = 67,2 (m2).
Tổng chi phí để sơn lại toàn bộ mặt ngoài của bức tường đó là:
67,2 ∙ 15 000 = 1 008 000 (đồng).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án (Phần 1)
-
135 câu Bài tập Hình học mặt nón, mặt trụ, mặt cầu cực hay có lời giải (P1)
-
79 câu Chuyên đề Toán 12 Bài 2 Dạng 1: Xác định vectơ pháp tuyến và viết phương trình mặt phẳng có đáp án
-
87 câu Chuyên đề Toán 12 Bài 3 Dạng 1: Xác định vectơ pháp tuyến và viết phương trình mặt phẳng có đáp án
-
80 câu Trắc nghiệm Tích phân có đáp án (Phần 1)
-
56 câu Chuyên đề Toán 12 Bài 2: Lôgarit có đáp án
-
15 câu Trắc nghiệm Số phức có đáp án (Vận dụng)
-
7 câu Trắc nghiệm Khối đa diện lồi và khối đa diện đều có đáp án (Vận dụng)
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận