Câu hỏi:

13/07/2024 138

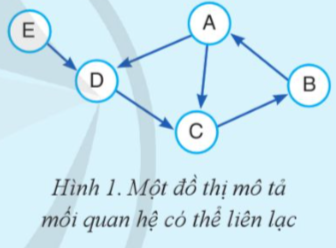
Có 5 bạn A, B, C, D và E, biết rằng A có số điện thoại của C và D, do đó A có thể liên lạc với C, D; tương tự B có số điện thoại của A; C có số điện thoại của B; D có số điện thoại của C; E có số điện thoại của D. Nếu biểu diễn A, B, C, D, E là các đỉnh của đồ thị và xét mối quan hệ có số điện thoại (có thể liên lạc), ta có đồ thị như Hình 1. Em hãy cho biết nếu A cần thông báo một thông tin thì những ai có thể nhận được thông tin đó. Câu hỏi tương tự nếu người cần thông báo thông tin là E.

Xem lời giải

Câu hỏi trong đề: Giải chuyên đề Tin 12 Cánh diều Bài 4: Duyệt đồ thị có đáp án !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

Có 5 bạn A, B, C, D và E, biết rằng A có số điện thoại của C và D, do đó A có thể liên lạc với C, D; tương tự B có số điện thoại của A; C có số điện thoại của B; D có số điện thoại của C; E có số điện thoại của D. Nếu biểu diễn A, B, C, D, E là các đỉnh của đồ thị và xét mối quan hệ có số điện thoại (có thể liên lạc), ta có đồ thị như Hình 1.

- Nếu A cần thông báo một thông tin thì C, D và B có thể nhận được thông tin đó.

- Nếu người cần thông báo thông tin là E thì người có thể nhận được thông tin đó là D,C,B,A.

Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

Bình luận

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Với các thông tin về tuyến xe buýt giữa các địa điểm được biểu diễn bằng ma trận kể như Hình 13. Em áp dụng thuật toán duyệt theo chiều rộng hoặc theo chiều sâu để chỉ ra các địa điểm có thế đến được nếu xuất phát địa điểm 0 và chỉ sử dụng các tuyến xe buýt này.

Xem đáp án

Lời giải

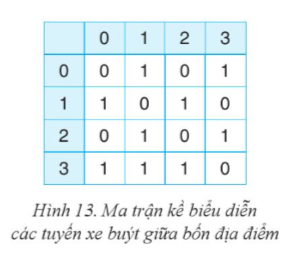
Với các thông tin về tuyến xe buýt giữa các địa điểm được biểu diễn bằng ma trận kể như Hình 13. Em áp dụng thuật toán duyệt theo chiều rộng hoặc theo chiều sâu để chỉ ra các địa điểm có thế đến được nếu xuất phát địa điểm 0 và chỉ sử dụng các tuyến xe buýt này như sau:

* Duyệt theo chiều rộng (BFS) như sau:

Chúng ta sẽ sử dụng BFS để tìm các địa điểm có thể đến được từ địa điểm 0.

- Khởi tạo: Đặt một hàng đợi để lưu trữ các địa điểm cần khám phá. Bắt đầu với địa điểm 0. Đánh dấu địa điểm 0 là đã được thăm. Tạo một danh sách để lưu trữ các địa điểm đã đến được.

- Thuật toán: Lặp lại cho đến khi hàng đợi rỗng:

+ Lấy địa điểm đầu tiên ra khỏi hàng đợi.

+ Khám phá tất cả các địa điểm kết nối trực tiếp với địa điểm hiện tại (theo ma trận kề).

+ Nếu địa điểm chưa được thăm, thêm nó vào hàng đợi và đánh dấu là đã thăm.

* Mã giả cho BFS

def bfs(graph, start):

visited = [False] * len(graph)

queue = []

reachable = []

queue.append(start)

visited[start] = True

while queue:

node = queue.pop(0)

reachable.append(node)

for i in range(len(graph[node])):

if graph[node][i] == 1 and not visited[i]:

queue.append(i)

visited[i] = True

return reachable

# Ma trận kề

graph = [

[0, 1, 0, 1],

[1, 0, 1, 0],

[0, 1, 0, 1],

[1, 1, 1, 0]

]

# Xuất phát từ địa điểm 0

start = 0

reachable_locations = bfs(graph, start)

print("Các địa điểm có thể đến được từ địa điểm 0:", reachable_locations)

Kết quả như sau: Các địa điểm có thể đến được từ địa điểm 0 là: [0, 1, 3, 2]

Câu 2

Trong các câu sau đây, những câu nào đúng khi nói về duyệt đồ thị?

a) Duyệt đồ thị theo chiều sâu giúp ta xác định các đỉnh có thể tới được từ một đinh bất kì.

b) Duyệt đồ thị theo chiều rộng không thể giúp ta xác định các đỉnh có thể tới được từ một đỉnh bất kì.

c) Thứ tự thăm các đỉnh khi thực hiện cách duyệt đồ thị theo chiều rộng và theo chiều sâu sẽ giống hệt nhau.

d) Để duyệt đồ thị theo chiều rộng chúng ta sử dụng hàng đợi, thăm các đỉnh theo nguyên tắc vào trước ra trước.

c) Để duyệt đồ thị theo chiều sâu chúng ta sử dụng ngăn xếp, thăm các đinh theo nguyên tắc vào sau ra trước.

Xem đáp án

Lời giải

a) Đúng. Vì DFS khởi đầu từ một đỉnh nguồn và thăm tất cả các đỉnh có thể đạt tới từ đỉnh đó bằng cách đi sâu vào các nhánh của đồ thị trước khi quay lại.

b) Sai. Vì BFS khởi đầu từ một đỉnh nguồn và thăm tất cả các đỉnh kề với nó trước khi di chuyển đến các đỉnh kề của các đỉnh đã thăm. Do đó, BFS cũng giúp xác định các đỉnh có thể tới được từ một đỉnh bất kì.

c) Sai. Vì thứ tự thăm các đỉnh của BFS và DFS khác nhau do cách thức duyệt của chúng khác nhau. BFS duyệt theo cấp độ (tầng), trong khi DFS duyệt theo nhánh.

d) Đúng. Vì BFS sử dụng hàng đợi (queue) để quản lý các đỉnh chờ thăm, và nó thực hiện theo nguyên tắc vào trước ra trước (FIFO).

e) Đúng. Vì DFS sử dụng ngăn xếp (stack) để quản lý các đỉnh chờ thăm, và nó thực hiện theo nguyên tắc vào sau ra trước (LIFO).

Vậy các câu đúng là a, d, e.

Xem thêm các câu hỏi khác »

Hỏi bài tập